Two capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
5C1=3C2
3C1=5C2
3C1=5C2=0
9C1=4C2
The correct Answer is:B
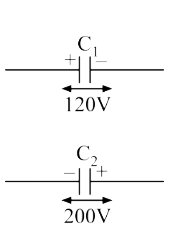
For potential to be made zero after connection, the charge both capacitors are equal
∴q1=q2
⇒C1V1=C2V2
⇒120C1=200C2⇒3C1=5C2 .
Similar Questions
Two capacitors of capacitance 10 μF and 20 μF are charged to potential 20 V and 10 V respectively. If they are connected to share charges, then loss of energy is
View SolutionTwo capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View Solution
Knowledge Check
Two insulated metallic spheres of 3μF and 5μF capacitances are charged to 300V and 500V respectively. The energy loss, when they are connected by a wire is
A400VB425VC350VD375VTwo capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
A5C1=3C2B8C1=5C2C9C1=5C2D3C1=5C2Two capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
A133.3VB150VC300VD400V
Two capacitors of capacitances 3μFand6μF, are charged to potentials 2V and 5V respectively. These two charged capacitors are connected in series. Find the potential across each of the two capacitors now.
View SolutionTwo capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
View SolutionTwo capacitors of 2μF and 3μF are charged to 150V and 120V, respectively. The plates of capacitor are connected as shown in the figure. An uncharged capacitor of capacity 1.5μF falls to the free end of the wire. Then
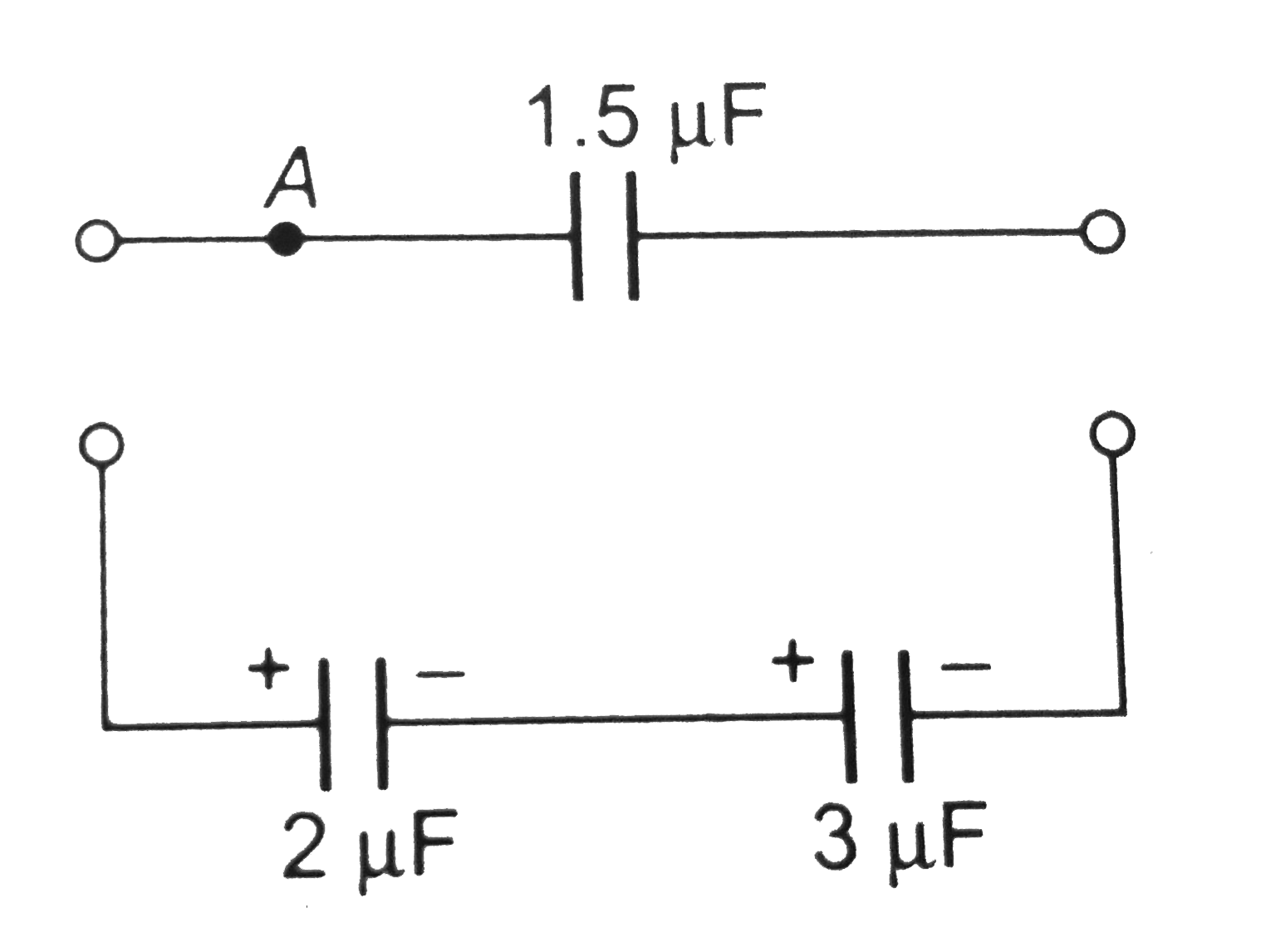
View SolutionTwo capacitors C1 and C2 are charged separately to potentials 20Vand10V, respectively. The terminals of capacitors C1andC2 are marked as (A-B) and (C-D), respectively. A is connected with CandB is connected with D.
i. Find the final potential difference across each capacitors.
ii. Find the final charge in both capacitors
iii. How much heat is produced in the circuit.
View SolutionTwo capacitors having capacities C1andC2 are charged to voltages V1andV2 respectively. There will be no exchange of energy in connecting them in parallel, if
View Solution
