A beaker containing a liquid of density moves up with an acceleration . The pressure due to the liquid at a depth h below the free surface of the liquid is.
The correct Answer is:B
Effective gravity
Similar Questions
Knowledge Check
The pressure in a liquid at a given depth below the surface :
Ais always exerted downward.Bis the same in all directions .Cequals the total weight of liquid above the depth.Ddepends upon the amount of liquid below the depth .A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
 A(a) MgB(b) Mg−VρgC(c) Mg+πR2hρgD(d) ρg(V+πR2h)
A(a) MgB(b) Mg−VρgC(c) Mg+πR2hρgD(d) ρg(V+πR2h)
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa
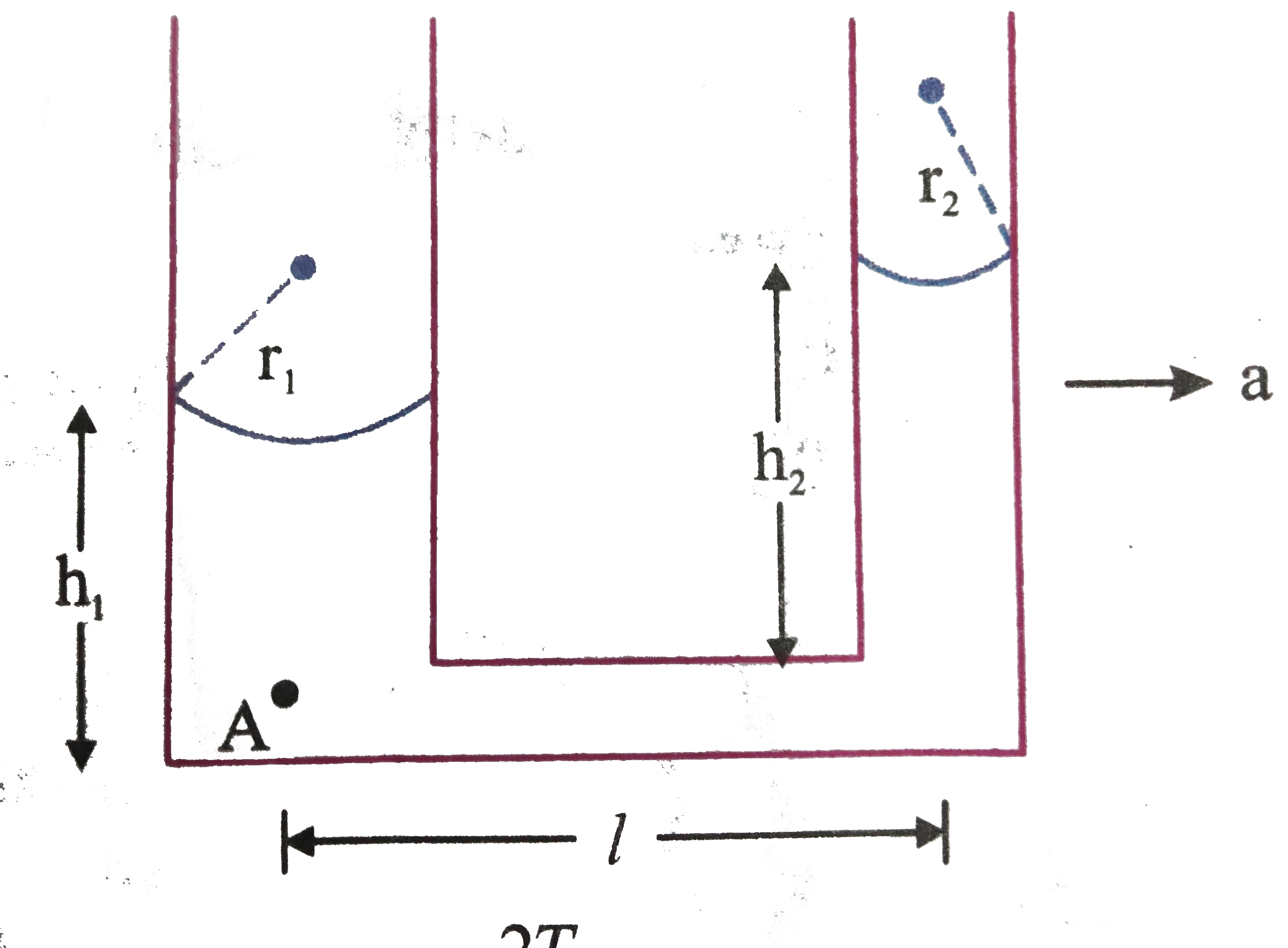
A vertical communicating tube contains a liquid of density ρ. If it moves with a horizontal acceleration a, pressure at A is equal to :
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is

View SolutionLiquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
View Solution
