A block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
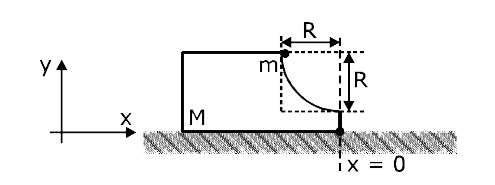
The velocity of the point mass m is: v= ⎷2gR1+mM
The velocity of the block M is: v=−mM√2gR
The position of the point mass is: x=−√2mRM+m
The x component of displacement of the center of mass of the block M is: −mRM+m
The correct Answer is:A, D
Net external force acting on the system along the x-axis is zero.
∴Along the x-axis
Momentum is conserved ⇒mv=MV
From conservation of energy
Loss in GPE of particle of mass m = Gain in kinetic energy of both the masses.
⇒mgh=12mv2+12MV2⇒mgh=12mv2+12M(mvM)2
⇒2gh=(1+mM)v2⇒v=
⎷2gh1+mM hence option (A) is correct.
V=mMv=m√2gh√M(m+M) along - ve x -axis.
Hence option [B] is incorrect.
Since the location of center of mass does not change along the x-axis.
mΔxm/G+MΔxM/G=0 (x+1)2+(y+2)2=1 m(R−x)−Mx=0f
x=mRm+M ΔxM/G=−mRm+M
Hence option (D) is correct.
Δxm/G=R−x=MRM+m
Final position of m=−x=−mRm+M
Hence option (C) is incorrect.
Similar Questions
Knowledge Check
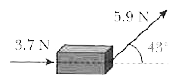
A block of mass √3kg rests on a horizontal frictionless surface. What will be the acceleration of the block if it is subjected to two forces as shown in the figure.
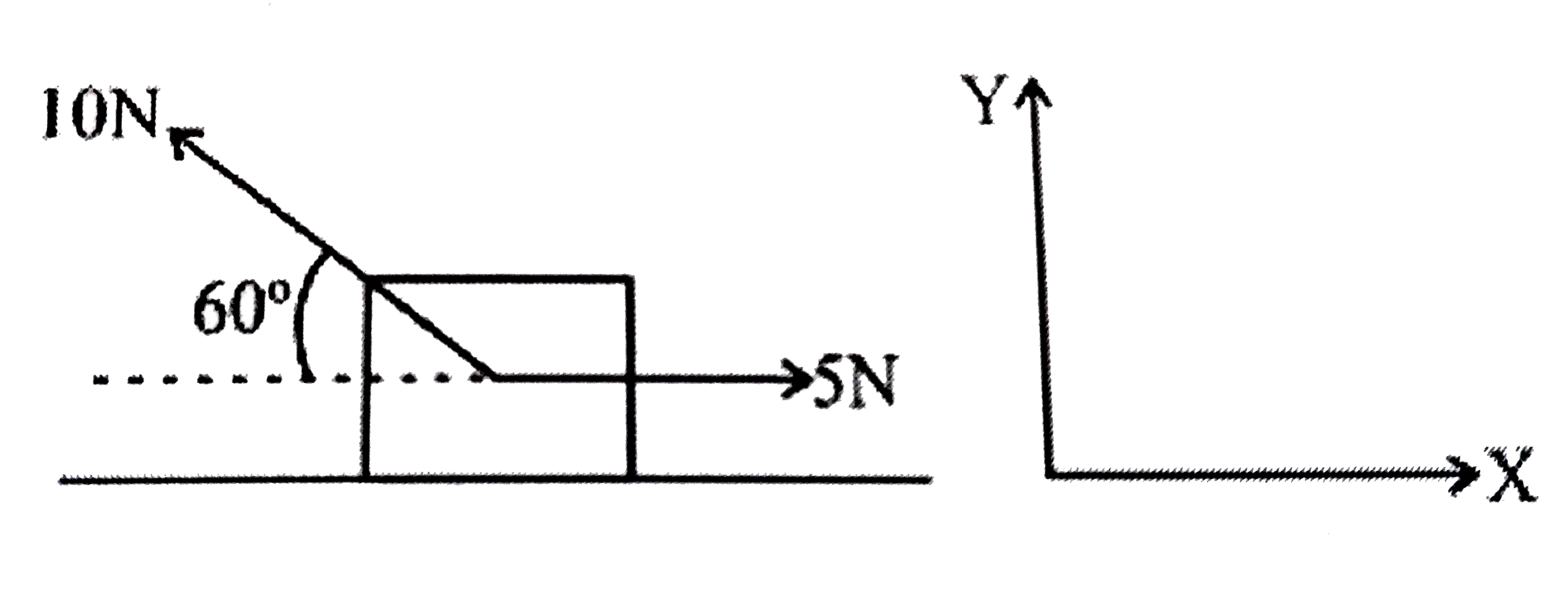 AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be there
AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be thereTwo blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the plane
Athe block A moves down the planeBthe block B moves down the planeCboth the blocks remain at restDboth the blocks move down the planeA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A2π√mK+√2LsinθgB2π√mK+√2(L−l)gsinθC2π√(L−l)gsinθ+√mKDnone of these
A block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given. What force is exerted by the rope on the block ?

View SolutionTwo forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
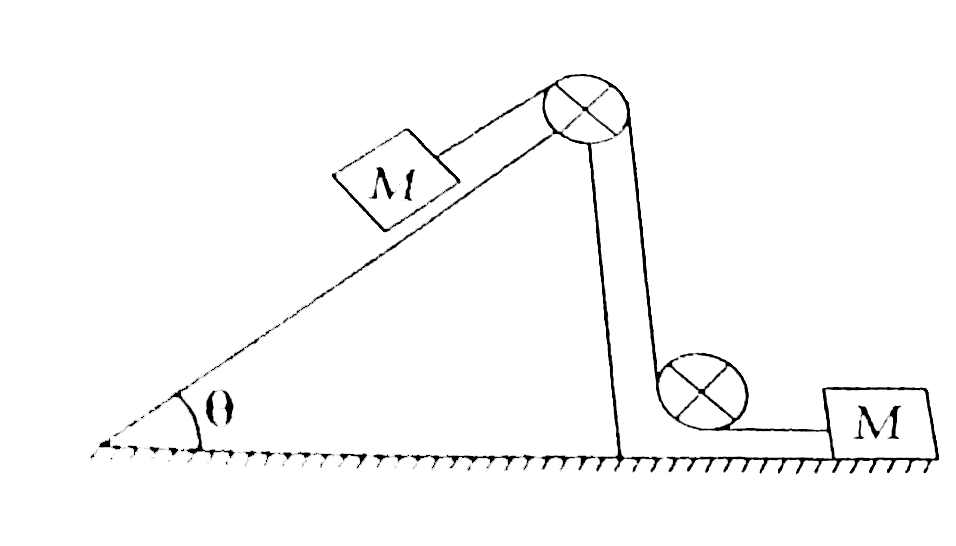
View SolutionTwo blocks, each having a mass M, rest on frictionless surfaces as shown in the figure. If the pulleys are light and frictionless and M on the incline is allowed to move down, then the tension in string will be
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution