Column-I gives operation of vectors →Aand→B and column- II gives the angle (θ) between →A and →B (→A and →B are not zero vectors ).

Video Solution
Text Solution
The correct Answer is:a→r,s;b→p;c→q;d→p
∣∣→A×→B∣∣=→A.→B
ABsinθ=ABcosθ
tanθ=1⇒θ=π/4or3π/4
(b) →A×→B=→B×→A only if θ=0∘
(c) ∣∣→A+→B∣∣=∣∣→A−→B∣∣
√A2+B2+2ABcosθ=√A2+B2−2ABcosθ
4ABcosθ=0
θ=π/2
(d) →A+→B=→C with A+B= C if θ=0∘.
|
Topper's Solved these Questions
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:INTERGER ANSWER
Explore 9 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:PASSAGE -1
Explore 3 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:ASSERTION- REASON
Explore 1 Video
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Link Compression
Explore 6 Videos
Similar Questions
Knowledge Check
If ∣∣→A+→B∣∣=∣∣→A−→B∣∣, then the angle between →Aand→B will be
Aθ=0Bθ=45∘Cθ=90∘Dθ=180∘The two vectors →A and →B are drawn from a common point and →C=→A+→B. Then, the angle between →A and →B is
A90∘ if C2>A2+B2Bgreater than 90∘ if C2<A2+B2Cgreater than 90∘ if C2>A2+B2Dless than 90∘ if C2>A2+B2The angle between vectors (→A×→B)and(→B×→A) is :
Aπ radBπ2 radCπ4 radDzero
Three vectors →A,→B,→C are shown in the figure. Find angle between
(i) →A and →B (ii) →B and →C (iii) →A and →C.
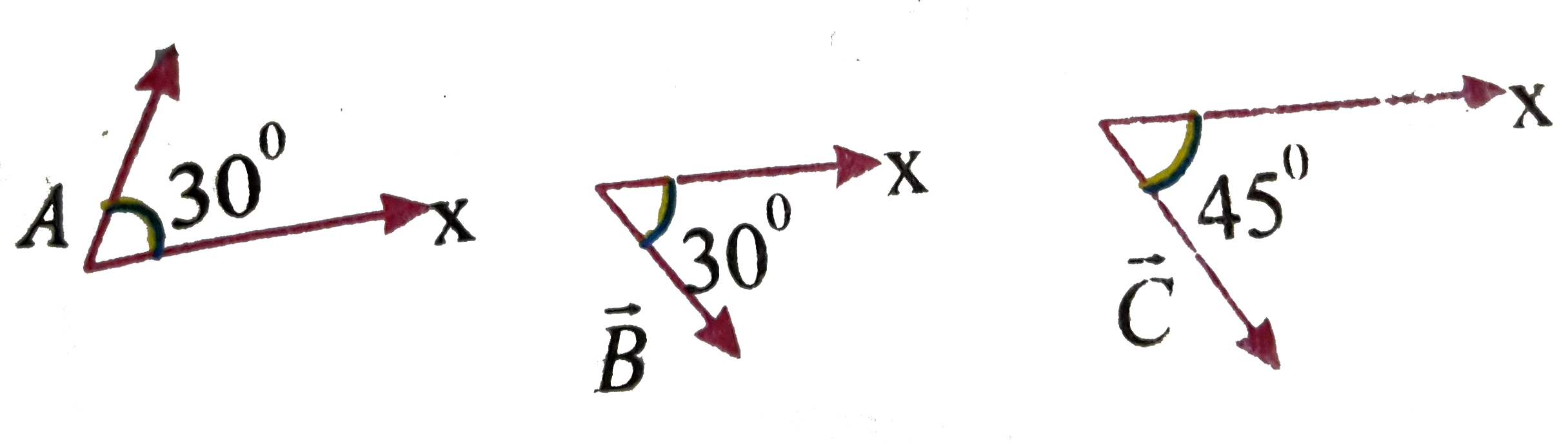
View SolutionThe two vectors →A and →B are drawn from a common point and →C=→A+→B. In column- I are given the conditions regarding the magnitudes of →A,→Band→C as A, B, C respectively. Column- II gives the angle between the vectors →Aand→B. Match them.

View SolutionIf →aand→b are two vectors such that ∣∣→a×→b∣∣=→a.→b, then what is the angle between →aand→b ?
View SolutionThe vector →A and →B are such that ∣∣→A+→B∣∣=∣∣→A−→B∣∣. The angle between vectors →A and →B is -
View SolutionIf →aand→b are two vector with |→a|=∣∣→b∣∣ and ∣∣→a+→b∣∣+2|→a|,then angle between →a and →b.
View Solution