The two vectors →A and →B are drawn from a common point and →C=→A+→B. In column- I are given the conditions regarding the magnitudes of →A,→Band→C as A, B, C respectively. Column- II gives the angle between the vectors →Aand→B. Match them.

Video Solution
Text Solution
The correct Answer is:a→r;b→p;c→q,s;d→p
(a) A2+B2=C2⇒θ=90∘
(b) A2+B2>C2⇒θ=90∘
A2+B2<C2⇒θ=90∘
(d) A2=B2=C2⇒θ=120∘⇒θ>90∘
|
Topper's Solved these Questions
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:INTERGER ANSWER
Explore 9 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:PASSAGE -1
Explore 3 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:ASSERTION- REASON
Explore 1 Video
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Link Compression
Explore 6 Videos
Similar Questions
Knowledge Check
The two vectors →A and →B are drawn from a common point and →C=→A+→B. Then, the angle between →A and →B is
A90∘ if C2>A2+B2Bgreater than 90∘ if C2<A2+B2Cgreater than 90∘ if C2>A2+B2Dless than 90∘ if C2>A2+B2The magnitudes of vectors →A,→Band→C are 3,4 and 5 units respectively. If →A+→B=→C, the angle between →A and →B is
Aπ2Bcos−1(0.6)Ctan−1(75)Dπ4A magnitude of vector →A,→B and →C are respectively 12,5 and 13 units and →A+→B=→C then the angle between →A and →B is
A0BπCπ/2Dπ/4
Vectors →A,→Band→C are shown in figure. Find angle between
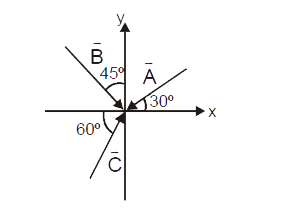
(i)→Aand→B (ii)→Aand→C (iii)→Band→C.
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionGiven : →C=→A+→B . Also , the magnitude of →A,→Band→C are 12,5 and 13 units respectively . The angle between →Aand→B is
View SolutionThe magnitudes of vectors →A.→B and →C are respectively 12,5 and 13 unira and →A+→B=→C, then the angle between →A and →B is :
View SolutionTwo vectors →a and →b add to give a resultant →c=→a+→b. In which of these cases angle between →a and →b is maximum: (a,b,c represent the magnitudes of respective vectors )
View Solution


