For the ellipse given by (x−3)225+(y−2)216=1, match the equations of the lines given in List I with those on the List Ii.
List IList IIi.The equation of the minor axisp.3x=34ii.The equation of a latusrectumr.x+y=9s.x=6f.x=3u.3y=34Solution in Telugu
I,P,S
Q,U,F
Q,P,F
Q,P,S
The correct Answer is:d
Step by step video, text & image solution for For the ellipse given by ((x - 3)^(2))/(25) + ((y - 2)^(2))/(16) = 1, match the equations of the lines given in List I with those on the List Ii. {:("List I","List II"),(i."The equation of the minor axis",p. 3 x = 34),(ii."The equation of a latusrectum",r. x + y = 9),( ,s. x = 6),( ,f. x = 3),( ,u. 3y = 34):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An equation of a line whose segment between the coordinates axes is divided by the point (12,13) in the ratio 2:3 is
View SolutionIf tan20∘=λ then show that tan160∘−tan110∘1+tan160∘.tan110∘=1−λ22λ.
View Solution(x-1) and (x+1) are factors of P(x)=ax3−bx2+2x−7. List-II represents remainder when P(x) is divided by entries of List-I. ∣∣ ∣ ∣ ∣ ∣ ∣∣List-IList-II(P)(x−2)(1)−92(Q)(x+2)(2)33(R)(2x−1)(3)−6(S)(2x+1)(4)9∣∣ ∣ ∣ ∣ ∣ ∣∣
View SolutionConsider the equation x2+p|x|+1=0, where p is real coefficient
Match List-I and List-II and select the correct answer using the code given below the list.
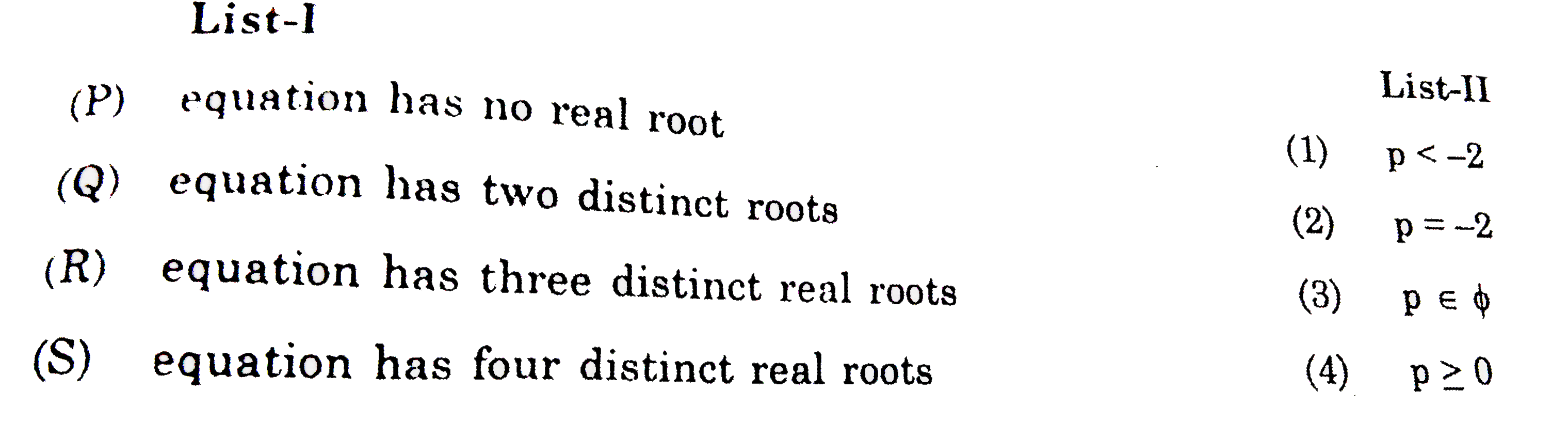
View SolutionLet f(x)=x2−6x+5x2−5x+6. Then match the expressions/statements in List I with expression /statements in List II.

View SolutionFor the ellipse given by (x−3)225+(y−2)216=1, match the equations of the lines given in List - I with those in the List - II

The correct matching is
View SolutionFor the circle C with the equation x2+y2−16x−12y+64=0 match the list-I with the list-II given below:
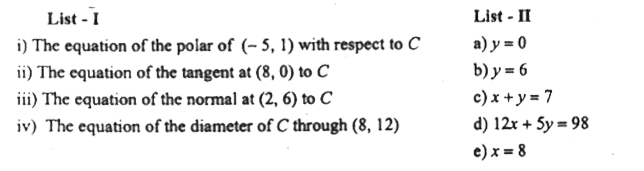
View SolutionFor the ellipse (x^(2))/(25)+(y^(2))/(16) = 1 , a list of lines given in List I are to be matched with their equation given in List II.
View SolutionLet x and y be positive real numbers such that y3+y≤x−x3 . Then match the following list -I with List- II Where [.] is greatest integer function.
List - I List - II(P)[x1x−y1y](1)−1(Q)[x1x−1](2) 0(R) [3−(1−x)2](3) 1(s) [x2−y2+1](4)2
View SolutionGiven the circle C with the equation x2+y2−2x+10y−38=0. Match the List I with the List II given below concerning C.
List IList IIA.The equation of the polar ofI.y+5=0(4, 3) with respect to CB.The equation of the tangent atII.x=1(9, -5) on CC.The equation of the normal atIII.3x+8y=27(-7, -5) on CD.The equation of the diameter ofIV.x+y=3C passing through (1, 3)V.x=9
The correct answer is
View SolutionFor the ellipse x225+y216=1 a list of lines given in List I are to be matched with their equations given in Lisht II.
The correct match is:
View SolutionList−IList−IIThe number of rational points on the ellipsex29+y24=14The number of integral points on the ellipsex29+y24=12The number of integral points on the ellipsex23+y21=1∞
View SolutionFor the ellipse x225+y216=1, a list of lines given in List-I are to be matched with their equation given in list II
listIlistIIdirectrix corresponding to the focus(−3,0)y=4tangent at the vertex(0,4)3x=25latus rectum through(3,0)x=3y+4=0x+3=03x+25=0
View SolutionMatch the following from List-I to List-II
list−Ilist−IImajor axis of3(x−12)+4(y+22)=12y−√2=0minor axis of2(x+12)+3(y−12)=6x−2√2=0directirx ofx2+2y2=4y+2=0latus rectum of2x2+y2=4x+1=0
View SolutionMatch the differential equations in List-I to their integrating factors in List-II
List - IList-II(i)(x3+1)dydx+x2y=0(a)x3(ii)x2dydx+3xy=x6(b)(x3+1)2(iii)(x3+1)dydx+6x2(x3+1)y=x2(c)(x2+1)2(iv)(x2+1)dydx+4xy=lnx(d)x2+1(e)(x3+1)13(f)(x3+1)12
The correct matching is
View Solution

