For the ellipse x225+y216=1, a list of lines given in List-I are to be matched with their equation given in list II
listIlistIIdirectrix corresponding to the focus(−3,0)y=4tangent at the vertex(0,4)3x=25latus rectum through(3,0)x=3y+4=0x+3=03x+25=0Solution in Telugu
b a e
f a c
b d c
f a e
The correct Answer is:B
Step by step video, text & image solution for For the ellipse (x^(2))/(25)+(y^(2))/(16) = 1, a list of lines given in List-I are to be matched with their equation given in list II {:(list I,list II),("directrix corresponding to the focus" (-3,0),y=4),("tangent at the vertex" (0,4),3x=25),("latus rectum through" (3,0),x=3),("" ,y+4=0 ),("" ,x+3=0),("" ,3x+25=0):} by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELLIPSEBOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - PRACTICE EXERCISE
65 Videos
- ELLIPSEBOOK - AAKASH SERIESCHAPTER - ELLIPSEEXERCISE - EXERCISE-I
52 Videos
- DIFFERENTIAL EQUATIONSBOOK - AAKASH SERIESCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Practice Exercise
62 Videos
- EXPONENTIAL SERIES BOOK - AAKASH SERIESCHAPTER - EXPONENTIAL SERIES EXERCISE - EXERCISE - III
8 Videos
Similar Questions
If length of the major axis is 8 and e = 1√2Axes are co-ordinate axes then equation of the ellipse is
View SolutionFocus (4, 0), e =12 , directrix is x -16 = 0. Then equation of the ellipse is
View SolutionThe degree and order of the differential equation [1+2(dydx)2]32=5d2ydx2 are
View Solution(1+3)loge3+1+322!(loge3)2+1+333!(loge3)3+.....∞ =
View SolutionConsider the equation x2+p|x|+1=0, where p is real coefficient
Match List-I and List-II and select the correct answer using the code given below the list.
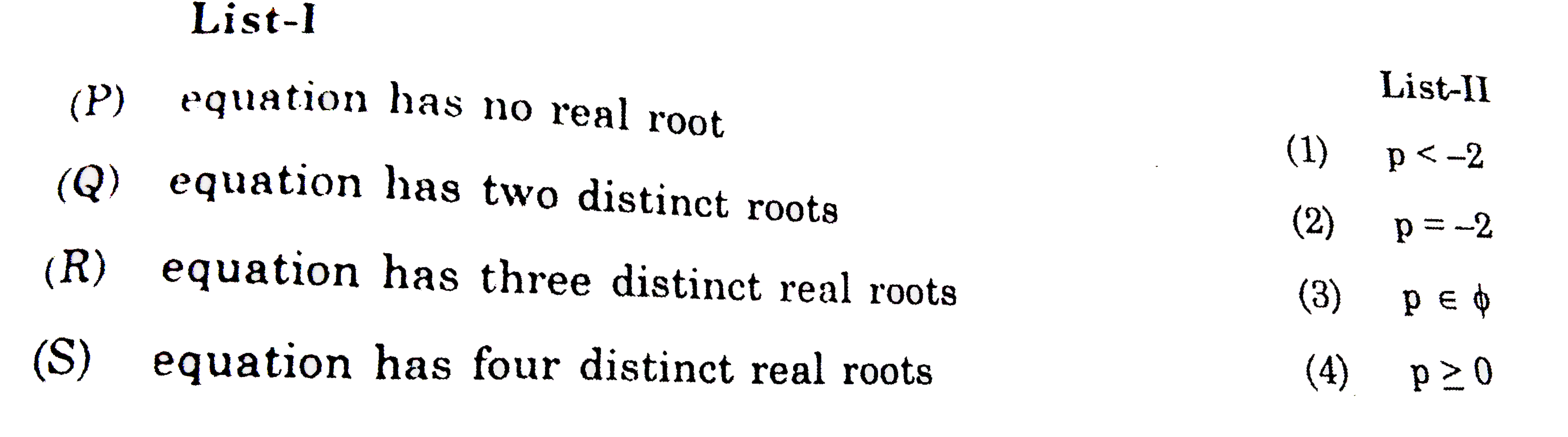
View SolutionFor the ellipse given by (x−3)225+(y−2)216=1, match the equations of the lines given in List - I with those in the List - II
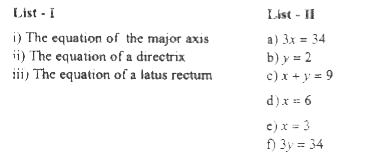
The correct matching is
View SolutionFor the circle C with the equation x2+y2−16x−12y+64=0 match the list-I with the list-II given below:
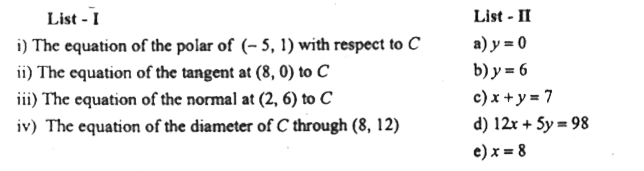
View SolutionGiven the circle C with the equation x2+y2−2x+10y−38=0 Match the List-I with the List-II given below concening C:

View SolutionFor the ellipse (x^(2))/(25)+(y^(2))/(16) = 1 , a list of lines given in List I are to be matched with their equation given in List II.
View SolutionFor the ellipse given by (x−3)225+(y−2)216=1, match the equations of the lines given in List I with those on the List Ii.
List IList IIi.The equation of the minor axisp.3x=34ii.The equation of a latusrectumr.x+y=9s.x=6f.x=3u.3y=34
View SolutionMatch the chemical conversions in List with the appropriate reagent in List II and select the correct answer using the code given below the lists: List I List II 1. (i) Hg(OAc)_2, (ii) NaBH_2 2. (i) alcKOH 3. Et-Br 4. (i) BH_3, (ii) H_2O_2//NaOH
View SolutionLet x and y be positive real numbers such that y3+y≤x−x3 . Then match the following list -I with List- II Where [.] is greatest integer function.
List - I List - II(P)[x1x−y1y](1)−1(Q)[x1x−1](2) 0(R) [3−(1−x)2](3) 1(s) [x2−y2+1](4)2
View SolutionGiven the circle C with the equation x2+y2−2x+10y−38=0. Match the List I with the List II given below concerning C.
List IList IIA.The equation of the polar ofI.y+5=0(4, 3) with respect to CB.The equation of the tangent atII.x=1(9, -5) on CC.The equation of the normal atIII.3x+8y=27(-7, -5) on CD.The equation of the diameter ofIV.x+y=3C passing through (1, 3)V.x=9
The correct answer is
View SolutionFor the ellipse x225+y216=1 a list of lines given in List I are to be matched with their equations given in Lisht II.
The correct match is:
View SolutionFor the parabola y2+2x+2y−3=0, match the items in List-I with those from List-II.

The correct match is
View Solution
