A bar of mass m resting on a smooth horizontal plane starts moving due to force
|F|=mg9. The magnitude of force remains
constant with time. The force vector makes an angle θ with the horizontal which varies with the distance covered as θ=Cx. if the
constant , C=10(degreemeter), then the speed of
the bar , when θ becomes equal to 30∘ for the first time is, (Take , g=10m/s2) Solution in Telugu
0.33 m/s
0.50 m/s
1.0 m/s
0.8 m/s
The correct Answer is:A
Figure shows a force acting on a bar,
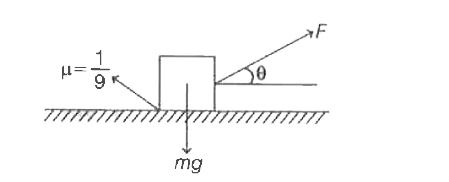
Since it is given that the minimum force to move the block ,
Fmin=mg9 ………(i)
So, the force acting on the bar
FH=Fcosθ=Fcos10x
Here, θ=cxandc=10∘m−1,θ=30∘
Hence at an angle 30∘ ,
θ=10x⇒30∘=10x⇒x=3m ........(ii)
Given that at 30∘ block start moving .
Hence , from Eq. (i) Fcos30∘=mg9
F=2mg9√3 ..........(iii)
From energy conservation law,
12mv2∣∣∣∫.cosθdx∣∣∣
Substituting the value F from Eq. (iii) we get
⇒12mv2=2mg9√3∣∣
∣∣3∫0cos10xdx∣∣
∣∣
12mv2=209√3m×sin30∘10∣∣∣
⇒v2=29√3⇒v=0.35≈0.33m/s
Topper's Solved these Questions
Similar Questions
Match the following fundamental forces of nature with their relative strength.
List-IList-II(A)Strong nuclear force(i)10−2(B)Weak nuclear force(ii)1(C)Elextromagnetic force(iii)10−39(D)Gravitational force(iv)10−13
The correct match is
View SolutionIdentify the correct option.
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg//3 of constant magnitude. In the process of its rectilinear motion the angle alpha between the direction of this force and the horizontal varies as alpha=as , where a is a constant, and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle alpha .
View SolutionPulling force making an angle θ to the horizontal is applied on a block of weight W placed on a horizontal table. If the angle of friction is α, then the magnitude of force is α , then the magnitude of force required to move the body is equal to
View SolutionA block of mass m resting on a smooth horizontal plane starts moving due to a constant force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle θ varies as θ=λs, where λ is constant and s is the distance traversed by the block from its intial position. Find the velocity of the block as a function of the angle θ. Also show that the block will never lose contact with the ground.
View SolutionAt the moment t=0 force F=kt is applied to a small body of mass m resting on a smooth horizontal plane (k is a constant) The direction of this force always forms an angle theta with the horizontal as shown. Find the time t at which moment, the body breaks off the plane:
View SolutionA bar of mass m_(1) is placed on a plank of mass m_(2) which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t_(0) at which the plank starts sliding is :
View Solutionएक व्यक्ति द्रव्यमान m के एक गुटके को एक चिकने आनत तल पर पकड़कर रखता है | आनत तल का क्षैतिज से झुकाव θ है | मनुष्य द्वारा लगाए गए बल F का परिमाण
View SolutionA block of mass m is lying on horizontal surface of coefficient of friction mu. A force is applied to the block at an angle theta with the horizontal. The block will move with a minimum force F if
View SolutionThe two wooden blocks move on a smooth horizontal plane in such a way that mass m remains constant relative to mass M as shown in the figure. The magnitude of force P is
View SolutionA body of mass m resting on a smooth horizontal plane starts moving under a constant force F. During its rectilinear motion, the angle theta between the direction of force and horizontal plane varies as 8 = kx , where k is a constant and x is the distance travelled by the body from the initial position. What is the velocity of the body?
View SolutionA body of weight 20N is on a horizontal surface, minimum force applied to pull it when applied force makes an angle 60∘ with horizontal (angle of friction θ=30∘) is
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA bar of mass m resting on a smooth horizontal plane starts moving due to the force F=mg/3 of constant magnitude. In the process of its rectilinear motion the angle alpha between the direction of this force and the horizontal varies as alpha =as, where a is a constant and s is the distance traversed by the bar from its initial position. Find the velocity of the bar as a function of the angle 'alpha'
View Solution
