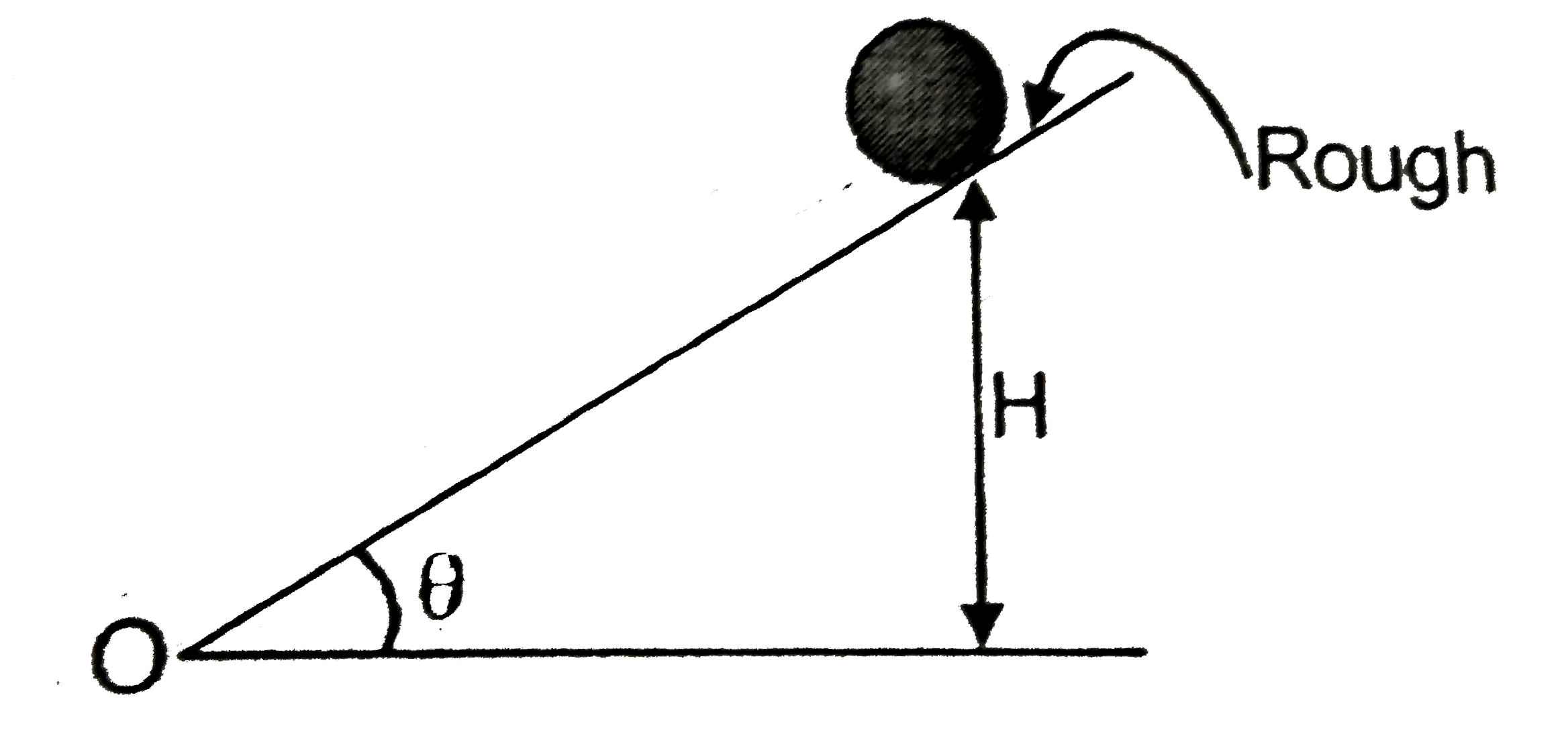
A solid spherical ball rolls on a horizontal surface at 10 m/s and continues to roll up on an inclined surface as shown in the figure.
If the mass of the ball is 11 kg and frictional losses are negligible, the value of h where the ball stop and starts rolling down the inclination is (Assume g=10m/s2 )
 Solution in Telugu
Solution in Telugu
8 m
6 m
7 m
10 m
The correct Answer is:C
Key Idea for rolling motion, the rotational kinetic energy is given by expression k
KE=12mv2(1+k2R2)
Given , rolling velocity on horizontal surface ,
VH=10m/s mass of ball , m= 11 kg and g=10m/s2 kinetic energy of rotation,
KE=12×11×(10)2⎛⎝1+25R2R2⎞⎠
(∵ For solid spherical ball ,k=√25R)
⇒=11×50×75J
By applying the law of energy conservation,
KEi+Vi=KEf+Vf
⇒11×50×75+0=0+mgh
⇒h=5010×75=7m
Topper's Solved these Questions
Similar Questions
Match the following fundamental forces of nature with their relative strength.
List-IList-II(A)Strong nuclear force(i)10−2(B)Weak nuclear force(ii)1(C)Elextromagnetic force(iii)10−39(D)Gravitational force(iv)10−13
The correct match is
View SolutionIdentify the correct option.
View SolutionA hollow spherical ball is given an initial push, up an incline of inclination angle α. The ball rolls purely coefficient of static friction between ball and incline =μ. During its upwards journey.
View SolutionA solid sphere rolls on a smooth horizontal surface at 10m/s and then rolls up a smooth inclined plane of inclination 30∘ with horizontal. The mass of the sphere is 2kg. Find the height attained by the sphere before it stops (in m).
View SolutionA one kg rolling on a smooth horizontal surface at 20ms−1 comes to the bottom of an inclined plane making an angle of 30∘ with the horizontal. Calculate K.E. of the ball when it is at the bottom of incline. How far up the incline will the ball roll ? Neglect friction.
View SolutionA solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
View Solutionएक गोला घर्षणयुक्त क्षैतिज सतह पर लुढ़क रहा है। यह धीरे-धीरे धीमा होकर रुक जाता है। घर्षण बल चेष्टा कर रहा है
View SolutionA uniform solid sphere rolls on a horizontal surface at 20 m/s. It, then, rolls up a plane inclined at
View SolutionA uniform solid sphere rolls on a horizontal surface at 20ms−1 . It then rolls up in incline having an angle of inclination at 30∘ with the horizontal . If the friction losses are negligible , the value of height h above the ground where the ball stops is
View Solutionएक चिकने क्षैतिज तल पर 2 किग्रा द्रव्यमान का एक ठोस गोला 10 मी/ से के वेग से लुढ़कने के बाद क्षैतिज से 30∘ अवनत चिकने सतह पर ऊपर की ओर लुढ़कते हुए आगे बढ़ता है , तो रुकने से पहले यह कितनी ऊँचाई तक ऊपर चढ़ जाएगा ?
View Solutionएक ठोस गोले का द्रव्यमान 2 किग्रा है। यह गोला 10 मी/से के वेग से एक चिकनी क्षैतिज सतह पर लोट (लुढ़क) (roll) रहा है और यह एक चिकने 30° के नत समतल पर लोटते (लुढ़कते) हुए चढ़ना प्रारम्भ करता है। इस गोले द्वारा अधिकतम प्राप्त ऊँचाई का मान होगा
(g = 9.8 मी/से2)
View Solutionएक 5 किग्रा. द्रव्यमान का ठोस गोला एक अनन्त धरातल पर बिना फिसले लुढ़क रहा है। धरातल का क्षैतिज से झुकाव 30∘ है तथा गुरूत्वीय त्वरण 9.8 मी./से.2 है। गोले का तल पर त्वरण ज्ञात कीजिये।
View Solutionएक ठोस गोला बिना फिसले एक क्षैतिज से 60∘ पर झुके नत समतल पर 10 मी दूरी तक लुढ़कता है। त्वरण (m/s2) में है
View SolutionA ball rolls down an inclined trck 2 m long in 4s. Find speed of the ball at the bottom of the track.
View SolutionAssuming a ball of mass m and of radius r to roll down from the top without slipping. Neglect energy losses due to rolling friction.
View Solution
