Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
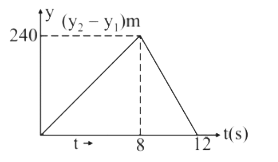

The correct Answer is:C
To solve the problem of the two stones thrown from a cliff, we need to analyze their motions and find the relative position of the second stone with respect to the first stone over time.
Step 1: Determine the equations of motion for both stones.
For Stone 1 (initial speed = 10 m/s):
- Initial height (h) = 240 m
- Initial velocity (u₁) = 10 m/s (upward)
- Acceleration (a) = -g = -10 m/s² (downward)
Using the equation of motion:
s1=u1t+12at2
Substituting the values:
s1=10t−12⋅10⋅t2
s1=10t−5t2
For Stone 2 (initial speed = 40 m/s):
- Initial velocity (u₂) = 40 m/s (upward)
Using the same equation of motion:
s2=u2t+12at2
Substituting the values:
s2=40t−5t2
Step 2: Calculate the time taken for each stone to hit the ground.
For Stone 1:
Setting the displacement equal to the height of the cliff:
240=10t−5t2
Rearranging gives:
5t2−10t−240=0
Dividing by 5:
t2−2t−48=0
Using the quadratic formula:
t=−b±√b2−4ac2a
Where a=1,b=−2,c=−48:
t=2±√(−2)2−4⋅1⋅(−48)2⋅1
t=2±√4+1922
t=2±142
The positive root gives:
t=8 seconds
For Stone 2:
Setting the displacement equal to the height of the cliff:
240=40t−5t2
Rearranging gives:
5t2−40t+240=0
Dividing by 5:
t2−8t+48=0
Using the quadratic formula:
t=8±√(−8)2−4⋅1⋅482⋅1
t=8±√64−1922
This gives no real solution, indicating that Stone 2 will also hit the ground after 8 seconds.
Step 3: Determine the relative position of Stone 2 with respect to Stone 1.
The relative position Y of Stone 2 with respect to Stone 1 is given by:
Y=s2−s1
Substituting the equations:
Y=(40t−5t2)−(10t−5t2)
Y=40t−10t
Y=30t
Step 4: Analyze the graph of relative position over time.
- From t=0 to t=8 seconds, the relative position Y increases linearly as 30t.
- After t=8 seconds, Stone 1 hits the ground, and Stone 2 continues to move upward until it reaches its peak and then falls back down.
Conclusion:
The best representation of the time variation of the relative position of the second stone with respect to the first stone will show a linear increase until t=8 seconds, followed by a downward parabolic motion after Stone 1 hits the ground.
- Initial height (h) = 240 m
- Initial velocity (u₁) = 10 m/s (upward)
- Acceleration (a) = -g = -10 m/s² (downward)
s1=u1t+12at2
Substituting the values:
s1=10t−12⋅10⋅t2
s1=10t−5t2
- Initial velocity (u₂) = 40 m/s (upward)
s2=u2t+12at2
Substituting the values:
s2=40t−5t2
Setting the displacement equal to the height of the cliff:
240=10t−5t2
Rearranging gives:
5t2−10t−240=0
Dividing by 5:
t2−2t−48=0
Using the quadratic formula:
t=−b±√b2−4ac2a
Where a=1,b=−2,c=−48:
t=2±√(−2)2−4⋅1⋅(−48)2⋅1
t=2±√4+1922
t=2±142
The positive root gives:
t=8 seconds
Setting the displacement equal to the height of the cliff:
240=40t−5t2
Rearranging gives:
5t2−40t+240=0
Dividing by 5:
t2−8t+48=0
Using the quadratic formula:
t=8±√(−8)2−4⋅1⋅482⋅1
t=8±√64−1922
This gives no real solution, indicating that Stone 2 will also hit the ground after 8 seconds.
Y=s2−s1
Substituting the equations:
Y=(40t−5t2)−(10t−5t2)
Y=40t−10t
Y=30t
- After t=8 seconds, Stone 1 hits the ground, and Stone 2 continues to move upward until it reaches its peak and then falls back down.
Similar Questions
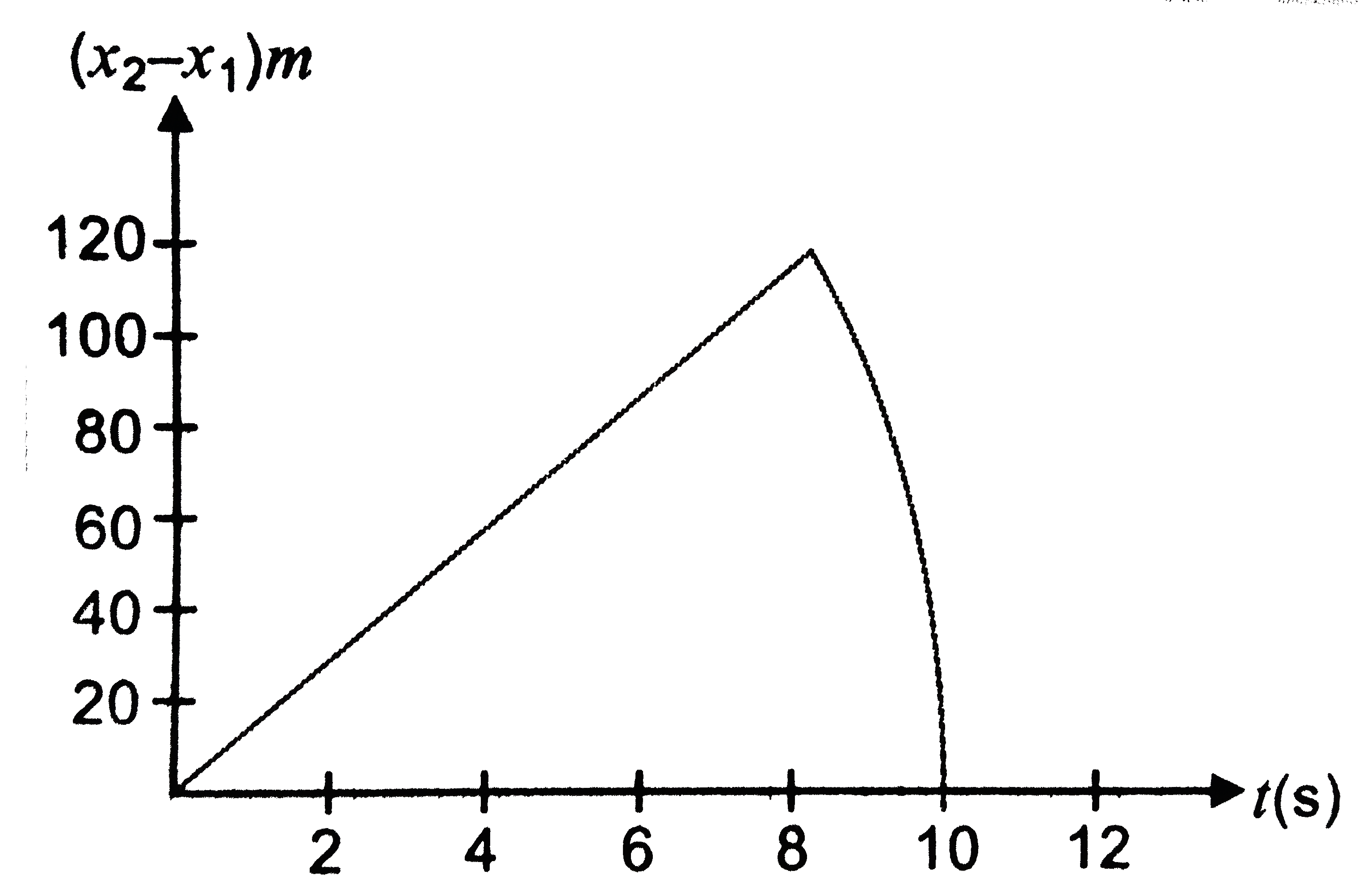
Two stones are thrown up simultaneously from the edge of a cliff 200m high with initial speeds of 15ms?−1 and 30−1. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relativ e position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Taje g=10ms−2.Give equations for the linear and curved parts of the plot.
 .
.
View SolutionTwo stones are thrown up simultaneously with initial speeds of u1 and u2(u2>1u1). They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Δx=(x2−x1) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.
View Solution
Knowledge Check
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A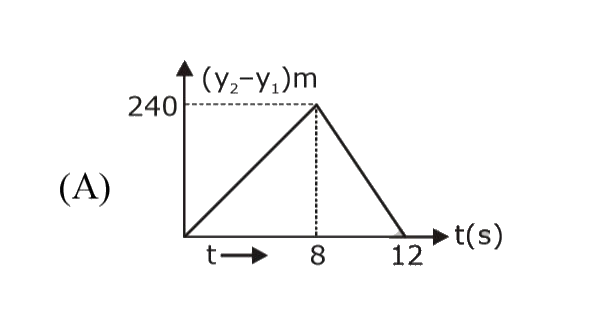 B
B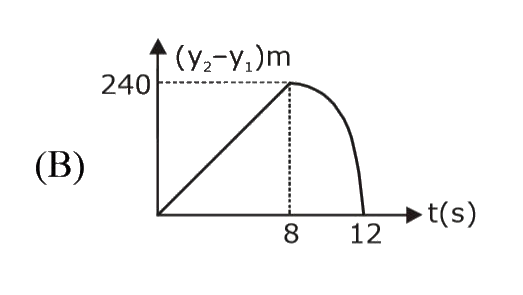 C
C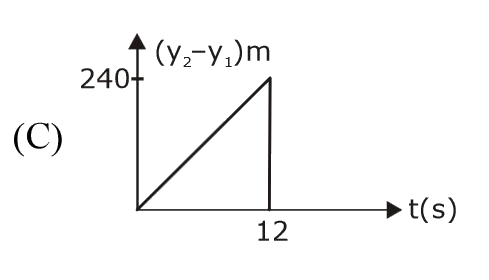 D
D
Two stones are thrown up simultaneously from the edge of a cliff 240m high with initial speed of 10m/sand40m/s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g=10m/s2)
( The figure are schematic and not drawn to scale )A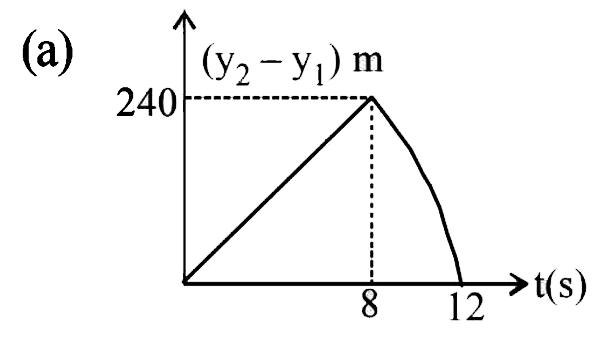 B
B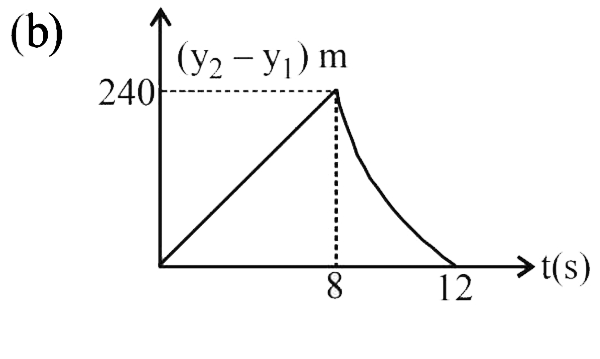 C
C D
D
Two stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone will request to the first as shown in the figure. The equation of the linear part is
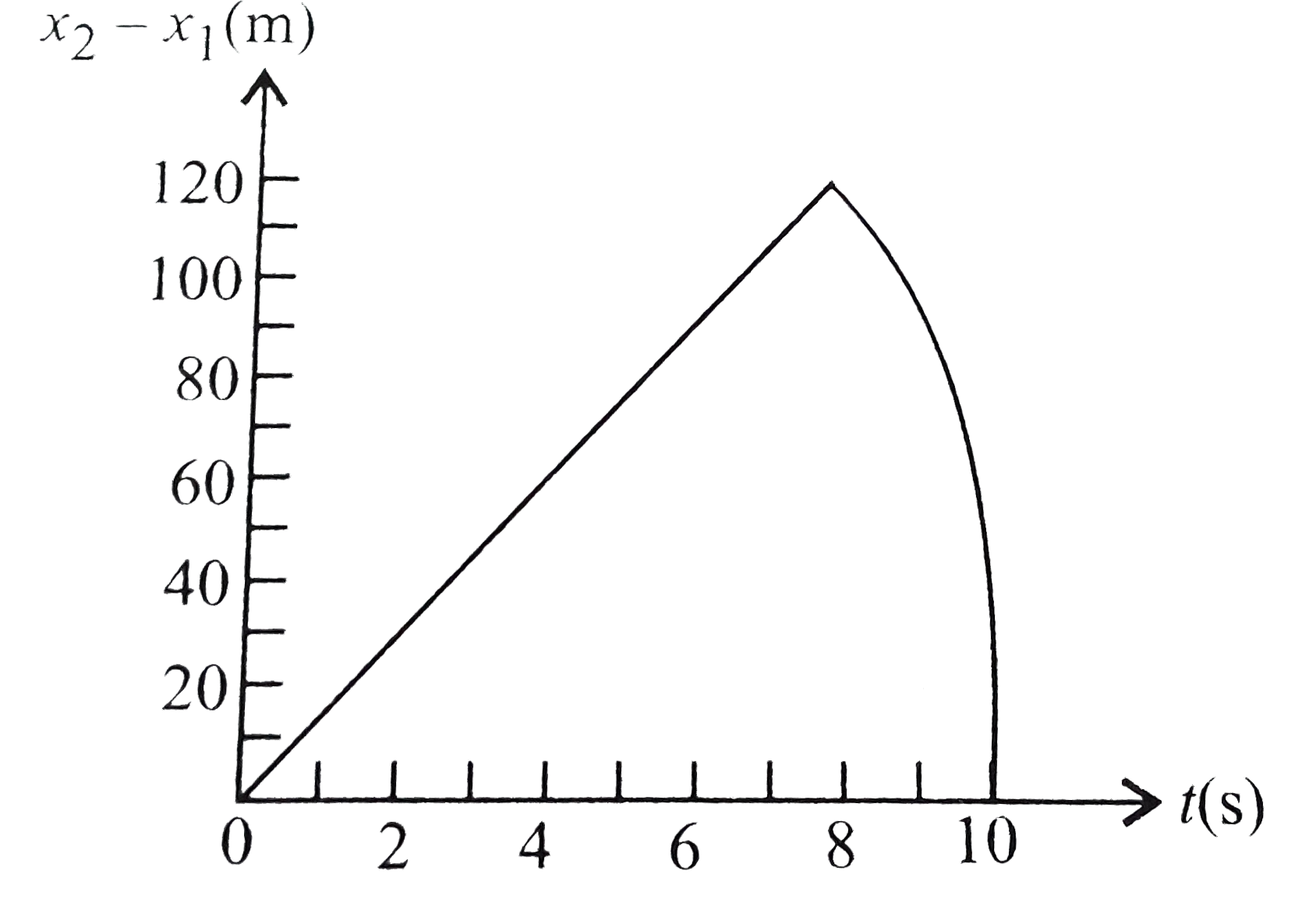 Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Ax2−x1 = 50tBx2−x1 = 10tCx2−x1 = 15tDx2−x1 = 20t
Two stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View SolutionTwo stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.
View SolutionA man standing on the edge of a cliff throws a stone straight up with initial speed (u) and then throws another stone straight down with same initial speed and from the same position. Find the relation of the speeds. The stones would have attained when they hit ground at the base of the cliff.
View Solution
