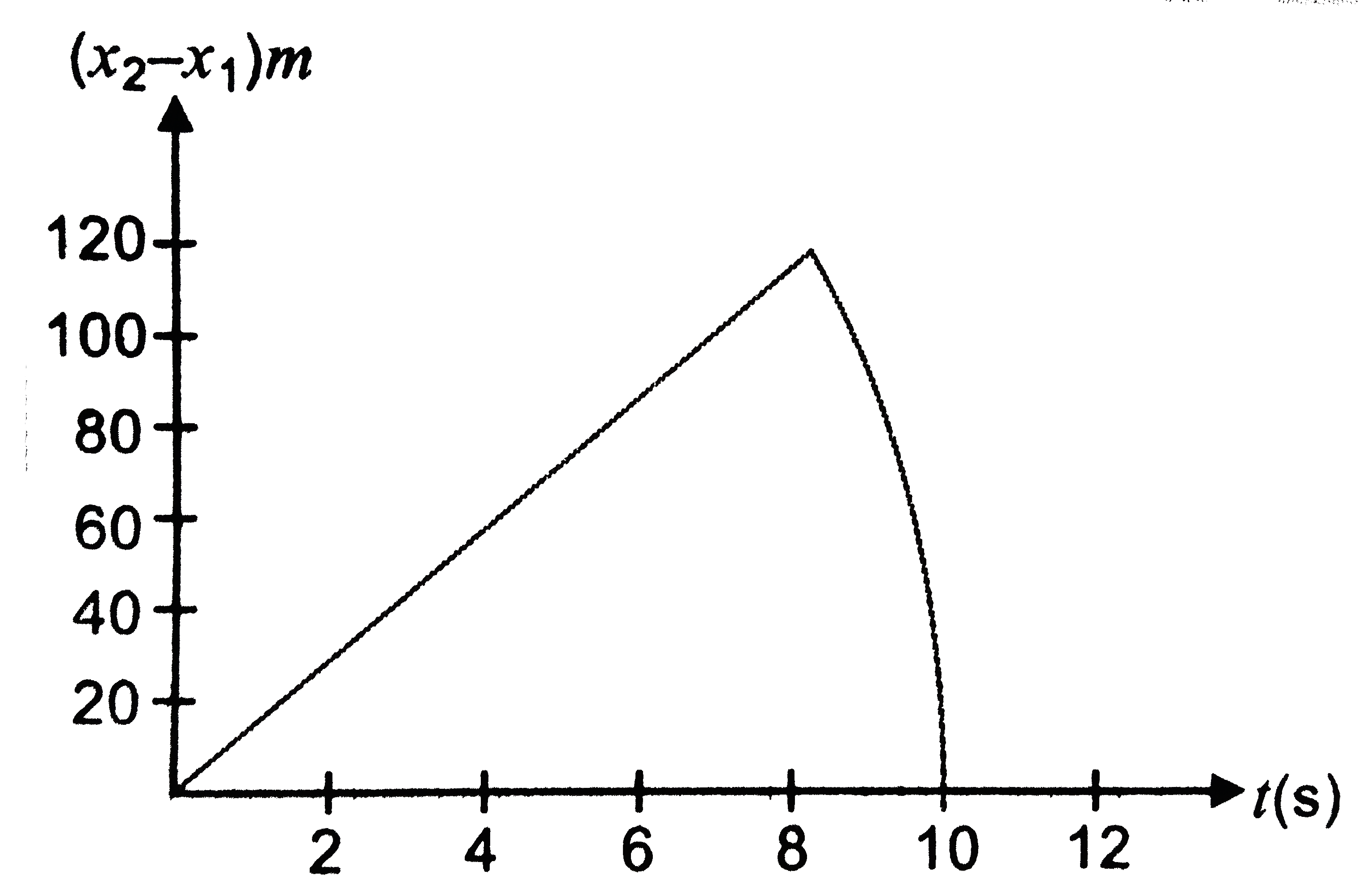
Two stones are thrown up simultaneously with initial speeds of u1 and u2(u2>1u1). They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Δx=(x2−x1) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.
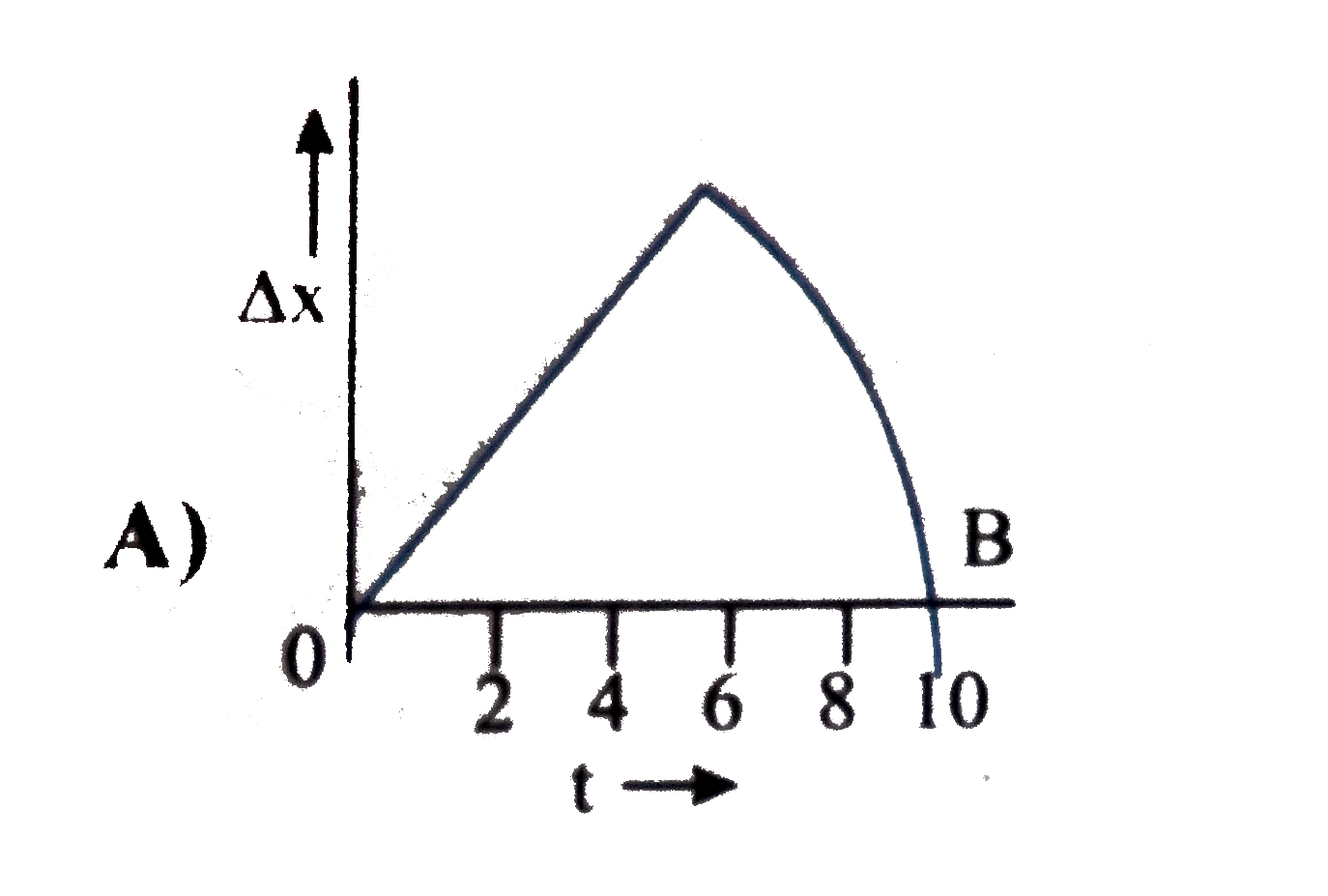
The correct Answer is:A
x1=u1t−12gt2
x2=u2t−12gt2
in is valid up t=6 sec only
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:More than One Option Question
Explore 7 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Passage Type Questions
Explore 16 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 3 C.W
Explore 25 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
Similar Questions
Two stones are thrown up simultaneously from the edge of a cliff 200m high with initial speeds of 15ms?−1 and 30−1. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relativ e position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Taje g=10ms−2.Give equations for the linear and curved parts of the plot.
 .
.
View SolutionTwo stones are thrown vertically upwards simultaneously with their initial velocities u1andu2 respectively. Prove that the heights reached by them would be in the ratio of u21:u22 (Assume upward acceleration is −g and downward acceleration to be +g).
View Solution
Knowledge Check
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A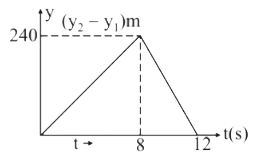 B
B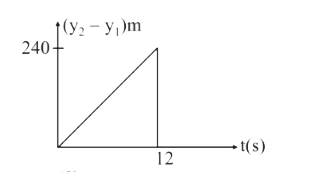 C
C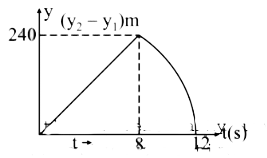 D
D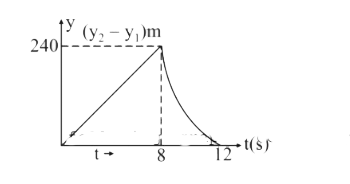
Two stones are thrown up simultaneously from the edge of a cliff 240m high with initial speed of 10m/sand40m/s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g=10m/s2)
( The figure are schematic and not drawn to scale )A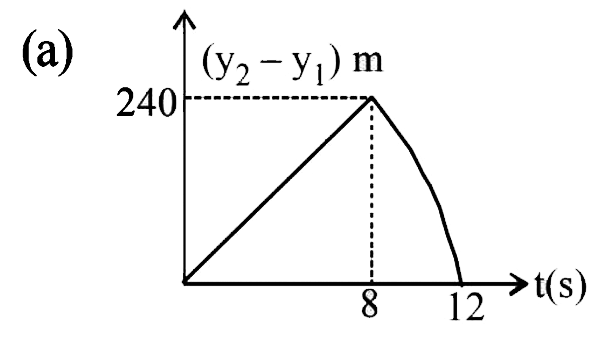 B
B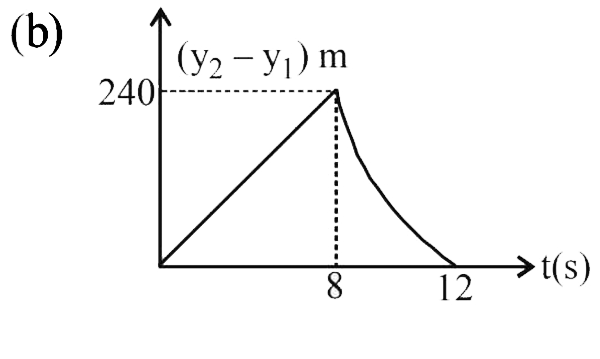 C
C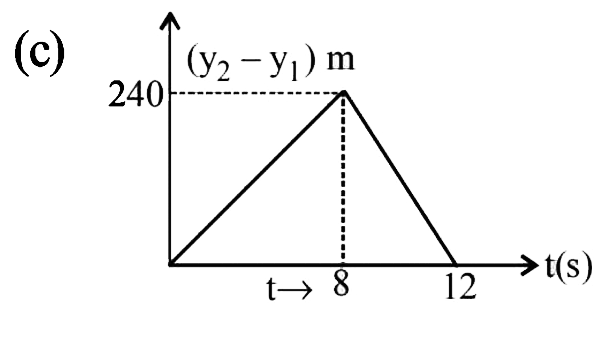 D
D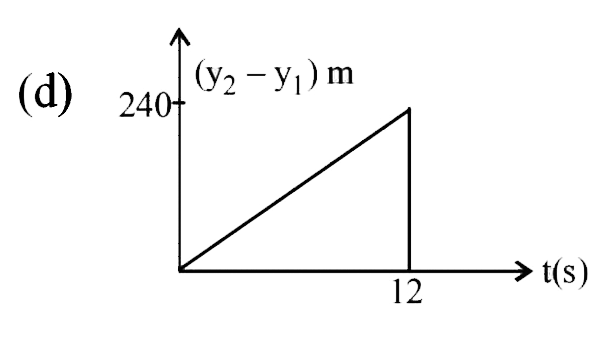
Two stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A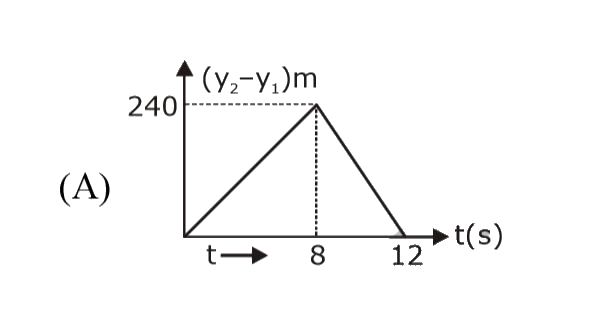 B
B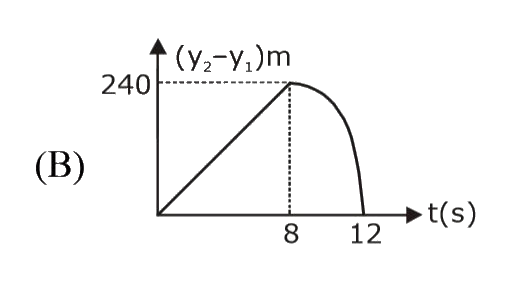 C
C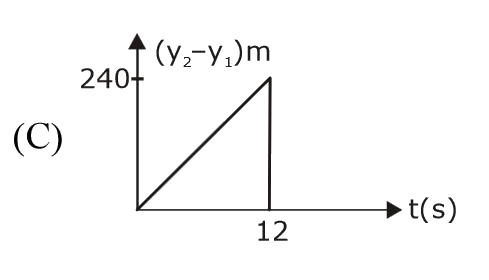 D
D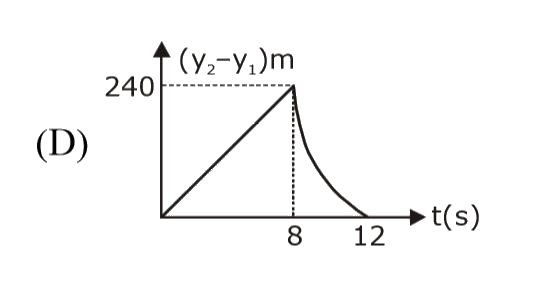
Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
(x2−x1) = the relative position of second stone with respect to first with time (t)
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
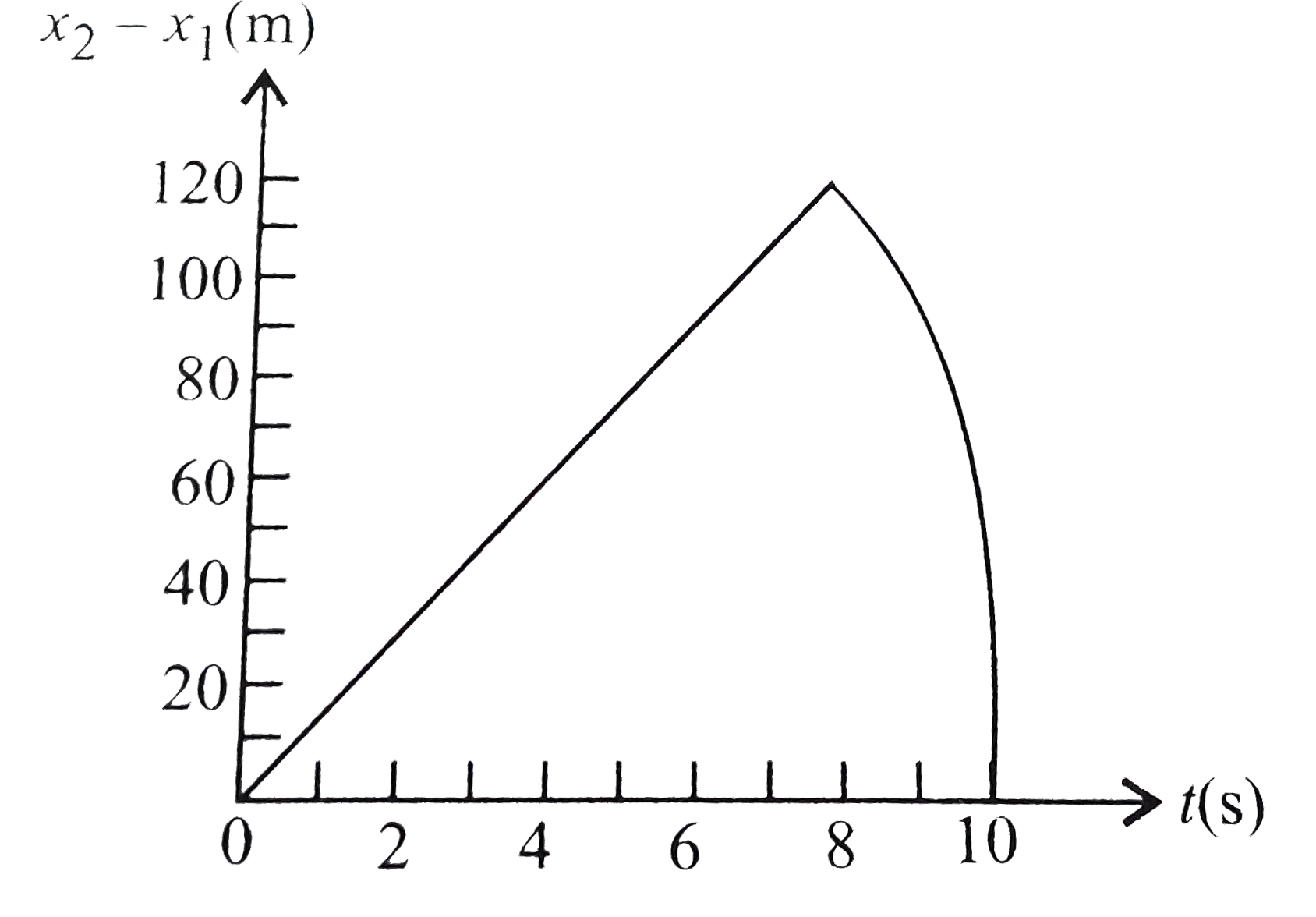
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone will request to the first as shown in the figure. The equation of the linear part is
View SolutionTwo particles are projected simultaneously in the same vertical plane from the same point, with different speeds u1 and u2, making angles θ1 and θ2 respectively with the horizontal, such that u1cosθ1=u2cosθ2. The path followed by one, as seen by the other (as long as both are in flight), is
View SolutionTwo particles are thrown simultaneously from points A and B with velocities u1=2ms−1andu2−14ms−1, respectively, as shown in figure.
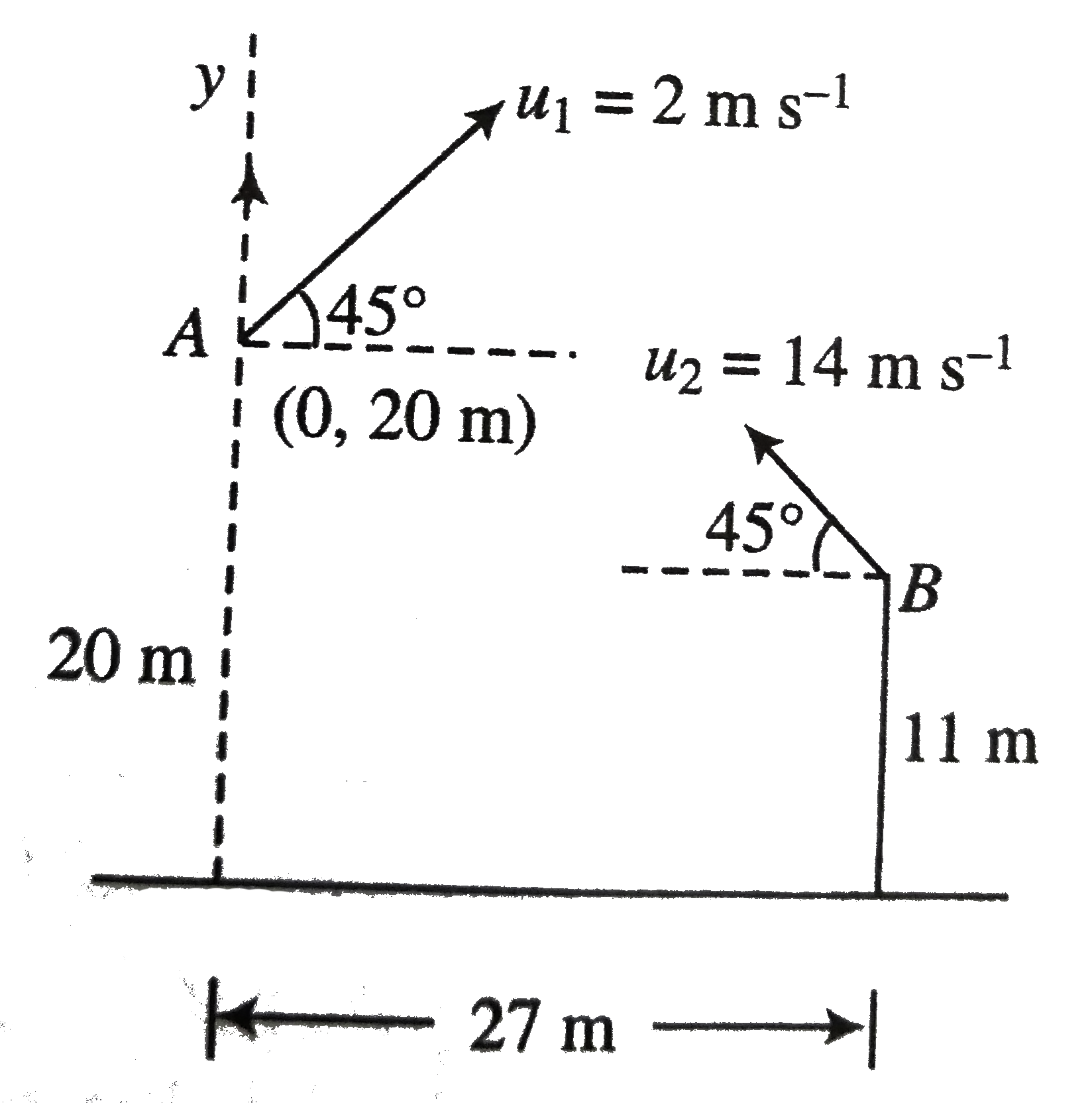
The relative velocity of B as seen from A in
View Solution

