A 2−m wide truck is moving with a uniform speed v0=8ms−1 along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed v when the truck is 4m away from him, The minimum value of v so that he can cross the road safely is .
2.62ms−1
4.6ms−1
3.57ms−1
1.414ms−1
The correct Answer is:C
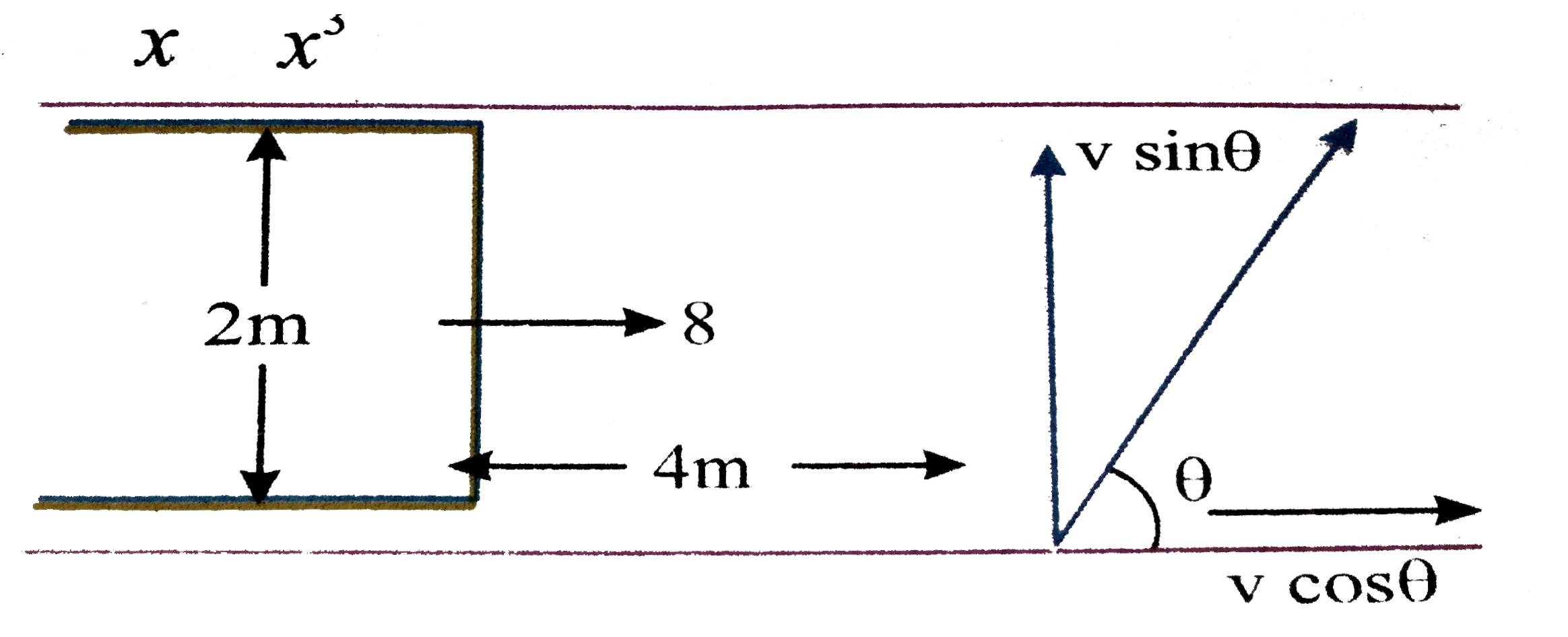
Time of crosing =2vsinθ
Time in which truck just able to catch the man=48−vcosθ
for safe crosing 2vsinθ=48−vcosθ
or 16−2vcosθ=4vsinθorv=48−vcosθ
For v minimum cosθ+2sinθ is maximum
so, ddθ(cosθ+2sinθ)=0
⇒−sinθ+2cosθ=0
⇒tanθ=2
⇒cosθ=1√5,sinθ=2√5
vmin=8√55=8√5
now =3.57m/s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - More than One Option Question
7 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Passage Type Questions
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 3 C.W
25 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
Similar Questions
A boy is moving with constant velocity v0on a straight road. When he is at a distance d behind the bus, the bus starts from rest and moves with a constant acceleration α. Find the minimum value of v0 so that the boy catches the bus.
View SolutionA truck is moving at a constant speed of 50km/h on a straight road which terminates on a wall. A fly starts moving with a constant speed of 100km/h from the wall towards the truck when the truck is at a distance 25km from the wall. Fly reaches the truck and then turns back towards the wall and then turns back towards the wall and then on reaching the wall it again turns towards the truck and so on. it makes several trips between the truck and the wall, before the truck just reaches the wall.
(a) What is the total distance travelled by the fly during this period?
(b) how many trips the fly makes between the truck and the wall?
View Solution
Knowledge Check
A 2−m wide truck is moving with a uniform speed v0=8ms−1 along a straight horizontal road. A pedestrian starts to cross the road with a uniform speed v when the truck is 4m away from him, The minimum value of v so that he can cross the road safely is .
A2.62 m/sB4.6 m/sC3.57 m/sD1.414 m/sA particle is moving at uniform speed 2ms−1 along a circle of radius 0.5m.The centripetal acceleration of particle is
A1ms−2B2ms−2C4ms−2D8ms−2A car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyre and the road is μ, the shortest distance in which the car can be stopped is.
Av202μgBv0μgC(v0μg)2Dv0μ
A boy is standing on a truck moving with a constant velocity of 15m/s on the horizontal road. The boy throws a ball in such a way that it returns to the truck after the truck has moved 60m. Find the speed and the angle of projection (a) as seen by the truck and (b) as seen from the road.
View SolutionA person is standing on a truck moving with a constant velocity of 14.7 m/s o a hrozontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection. a. as seen from the truck b. as seen fromt the road.
View SolutionA car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionTwo cars are moving with speed v1,v2 towards a crossing along two roads. If their distance from the crossing be 40 metres and 50 metres at an instant of time then they do not collide if their speed are such that
View SolutionA van is moving with a speed of 108 km / hr on level road where the coefficient of fraction between the tyres and the road is 0.5 for the safe driving of the van , the minimum radius of curvature of the road will be ( g=10m/s2)
View Solution
