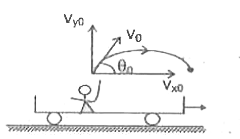
A boy is standing on a truck moving with a constant velocity of 15m/s on the horizontal road. The boy throws a ball in such a way that it returns to the truck after the truck has moved 60m. Find the speed and the angle of projection (a) as seen by the truck and (b) as seen from the road.
To solve the problem, we need to analyze the motion of the ball from two different reference frames: the truck (which is moving) and the ground (which is stationary).
Step 1: Analyze the motion from the ground frame
1. Given Data:
- Velocity of the truck, vt=15m/s
- Distance moved by the truck, d=60m
- Time taken, t
2. Calculate the time taken for the truck to move 60 m:
t=dvt=60m15m/s=4s
Step 2: Determine the horizontal component of the ball's velocity
1. Horizontal motion:
- The horizontal component of the ball's velocity, ucosθ, must equal the velocity of the truck since the ball returns to the truck.
ucosθ=vt=15m/s
Step 3: Determine the vertical component of the ball's velocity
1. Vertical motion:
- The vertical displacement of the ball after 4 seconds must be zero (it returns to the same height).
- Using the equation of motion:
0=usinθ⋅t−12gt2
where g≈10m/s2.
0=usinθ⋅4−12⋅10⋅(42)
usinθ⋅4=80
usinθ=20m/s
Step 4: Solve for u and θ
1. We now have two equations:
- ucosθ=15
- usinθ=20
2. Divide the two equations:
usinθucosθ=2015⟹tanθ=43
θ=tan−1(43)≈53∘
3. Calculate u:
- From ucosθ=15:
u=15cos(53∘)≈150.6=25m/s
Step 5: Analyze the motion from the truck frame
1. In the truck frame:
- The boy throws the ball vertically upwards, so the angle of projection is 90∘.
- The vertical component of velocity is usinθ=20m/s.
- The horizontal component of velocity is 0 (since the truck is the reference frame).
Final Answers
- (a) As seen by the truck:
- Speed: 20m/s
- Angle of projection: 90∘
- (b) As seen from the road:
- Speed: 25m/s
- Angle of projection: 53∘
1. Given Data:
- Velocity of the truck, vt=15m/s
- Distance moved by the truck, d=60m
- Time taken, t
t=dvt=60m15m/s=4s
1. Horizontal motion:
- The horizontal component of the ball's velocity, ucosθ, must equal the velocity of the truck since the ball returns to the truck.
ucosθ=vt=15m/s
1. Vertical motion:
- The vertical displacement of the ball after 4 seconds must be zero (it returns to the same height).
- Using the equation of motion:
0=usinθ⋅t−12gt2
where g≈10m/s2.
0=usinθ⋅4−12⋅10⋅(42)
usinθ⋅4=80
usinθ=20m/s
1. We now have two equations:
- ucosθ=15
- usinθ=20
usinθucosθ=2015⟹tanθ=43
θ=tan−1(43)≈53∘
- From ucosθ=15:
u=15cos(53∘)≈150.6=25m/s
1. In the truck frame:
- The boy throws the ball vertically upwards, so the angle of projection is 90∘.
- The vertical component of velocity is usinθ=20m/s.
- The horizontal component of velocity is 0 (since the truck is the reference frame).
- (a) As seen by the truck:
- Speed: 20m/s
- Angle of projection: 90∘
- Speed: 25m/s
- Angle of projection: 53∘
Topper's Solved these Questions
Similar Questions
A person is standing on a truck moving with a constant velocity of 14.7 m/s o a hrozontal road. The man throws a ball in such a way that it returns to the truck after the truck has moved 58.8 m. Find the speed and the angle of projection. a. as seen from the truck b. as seen fromt the road.
View SolutionA boy is standing inside a train moving with a constant velocity of magnitude 10 m/s. He throws a ball vertically up with a speed 5 m/s relative to the train. Find the radius of curvature of the path of the L ball just at the time of projection.
View Solution
Knowledge Check
A person is standing on an open car moving with a constant velocity of 30m/s on a striaght upward direction and it returns to person after the car has moved 240m. The speed and the angle of projection
Aas seen from the car is 40m/s, 90∘Bas seen from the road is 50m/s, tan−1(4/3)Cboth (1) and (2)DnoneA car is moving horizontally along a straight line with a unifrom velocity of 25ms−1. A projectile is to be fired from this car in such a way that it will return to it after it has moved 100m. The speed of the projection must be.
A10ms−1B20ms−1C15ms−1D25ms−1A truck is moving with a constant velocity of 54kmh−1. In which direction (angle with the direction of motion of truck) should a stone be projected up with a velocity of 20ms−1, from the floor of the truck of the truck, so as to appear at right angles to the truck, for a person standing on earth ?
Acos−2(−34)Bcos−1(−14)Ccos−1(23)Dcos−1(34)
An automobile and a truck start from rest at the same instant, with the automobile initially at some distance behind the truck. The truck has a constant acceleration of 2.2m/s2 and the automobile has an acceleration of 3.5m/s2. The automobile overtakes the truck when it (truck) has moved 60 m.
(a) How much time does it take the automobile to overtake the truck ?
(b) How far was the automobile behind the truck initially ?
(c) What is the speed of each during overtaking ?
View SolutionA truck starts from origin, accelerating with ams−2 in positive x - axis direction. After 2s, a man standing at the starting point of the truck projected a ball at an angle 30∘ with velocity vms−1. Find the relation between aandv such that the ball hits the truck. (Assume that truck is moving on horizontal plane and the man projected the ball from the same horizontal level of truck).
View SolutionA truck is moving at a constant speed of 50km/h on a straight road which terminates on a wall. A fly starts moving with a constant speed of 100km/h from the wall towards the truck when the truck is at a distance 25km from the wall. Fly reaches the truck and then turns back towards the wall and then turns back towards the wall and then on reaching the wall it again turns towards the truck and so on. it makes several trips between the truck and the wall, before the truck just reaches the wall.
(a) What is the total distance travelled by the fly during this period?
(b) how many trips the fly makes between the truck and the wall?
View SolutionA boy is sitting in a car moving with uniform velocity. The boy throws a ball vertically upwards which falls back into his hands. A man standing on the road watches the motion of the ball. The path of the motion of the ball will be:
View SolutionA heavy truck moving with a velocity of 60km/h collides with a light drum at rest. If the collision is elastic, then the velocity of the drum immediately after collision will be
View Solution

