Two stones are thrown vertically upwards simultaneously from the same point on the ground with initial speed u1=30m/sec and u2=50m/sec. Which of the curve represent correct variation (for the time interval in which both reach the ground) of
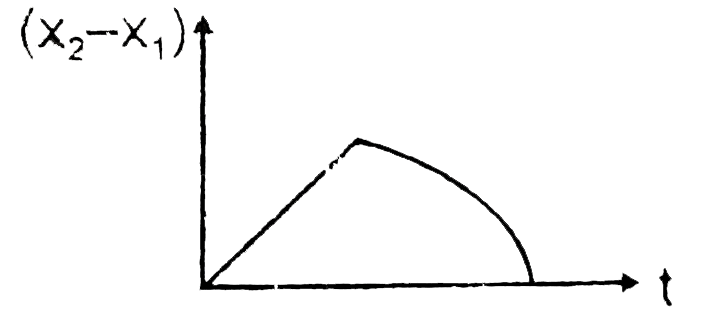
(x2−x1) = the relative position of second stone with respect to first with time (t)
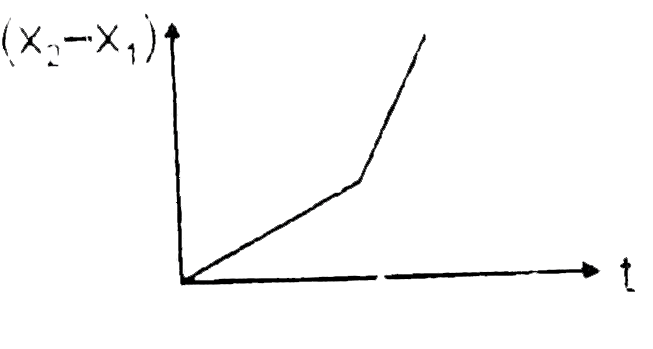
(v2−v1) = the relative velocity of second stone with respect to first with time (t).
Assuming that stones do not rebound after hitting.


The correct Answer is:A, D
While both the stones are in flight a1=g and a2=g
So arel=0⇒Vrel = constant
⇒xrel= (const) t
⇒ Curve of xrelv/st will be straight line. Xrel will be straight line.
After the first particle drops on ground, the seperation (xrel) will decrease parabolically (due to gravitational acceleration) and finally becomes zero.
and Vrel = slope of xrelv/st
xrelt
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.19
Explore 20 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.20
Explore 9 Videos
- DAILY PRACTICE PROBLEMBook:RESONANCEChapter:DAILY PRACTICE PROBLEMExercise:DPP No.17
Explore 20 Videos
- CURRENT ELECTRICITYBook:RESONANCEChapter:CURRENT ELECTRICITYExercise:High Level Problems (HIP)
Explore 21 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCEChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
Similar Questions
Knowledge Check
Two stones are thrown up simultaneously from the edge of a cliff with initial speed vand2v. The relative position of the second stone with respect to first varies with time till both the stones strike the ground as.
AlinearlyBfirst linearly then parabolicallyCparabolicallyDfirst parabolically then linearly
(assume that the first stone comes to rest after striking the ground).A stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
A3u2gB4u2gC6u2gD9u2gTwo stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
A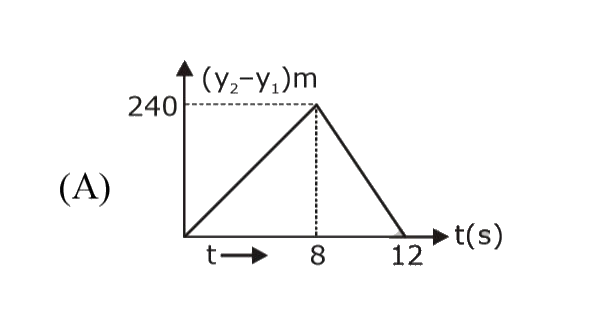 B
B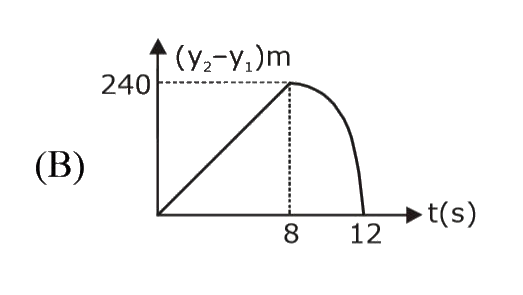 C
C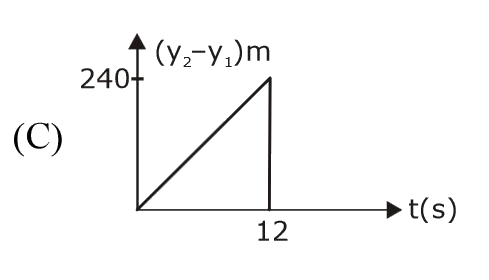 D
D
A stone is thrown vertically upwards with a velocity of 4.9ms−1. Calculate : the velocity with which it returns to the ground.
View SolutionTwo stones are thrown up simultaneously with initial speeds of u1 and u2(u2>1u1). They hit the ground after 6 s and 10 s respectively. Which graph in fig. correctly represents the time variation of Δx=(x2−x1) the relative position of the second stone with respect to the first upto t=10 s? Assume that the stones do not rebound after hitting the ground.
View SolutionTwo stones are through up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graphs best represents the time variation of relative position of the second stone with respect to the first? Assume stones do not rebound after hitting the ground and neglect air resistance, take . g=10m/s2 (The figures are schematic and not drawn to scale)
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 240m high with initial speed of 10m/sand40m/s respectively . Which of the following graph best represents the time variation of relative position of the speed stone with respect to the first ?
( Assume stones do not rebound after hitting the groumd and neglect air resistance , take g=10m/s2)
( The figure are schematic and not drawn to scale )
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff 200 m high with initial speeds of 15ms−1 and 30ms−1 respectively. The time variation of the relative position of the second stone will request to the first as shown in the figure. The equation of the linear part is
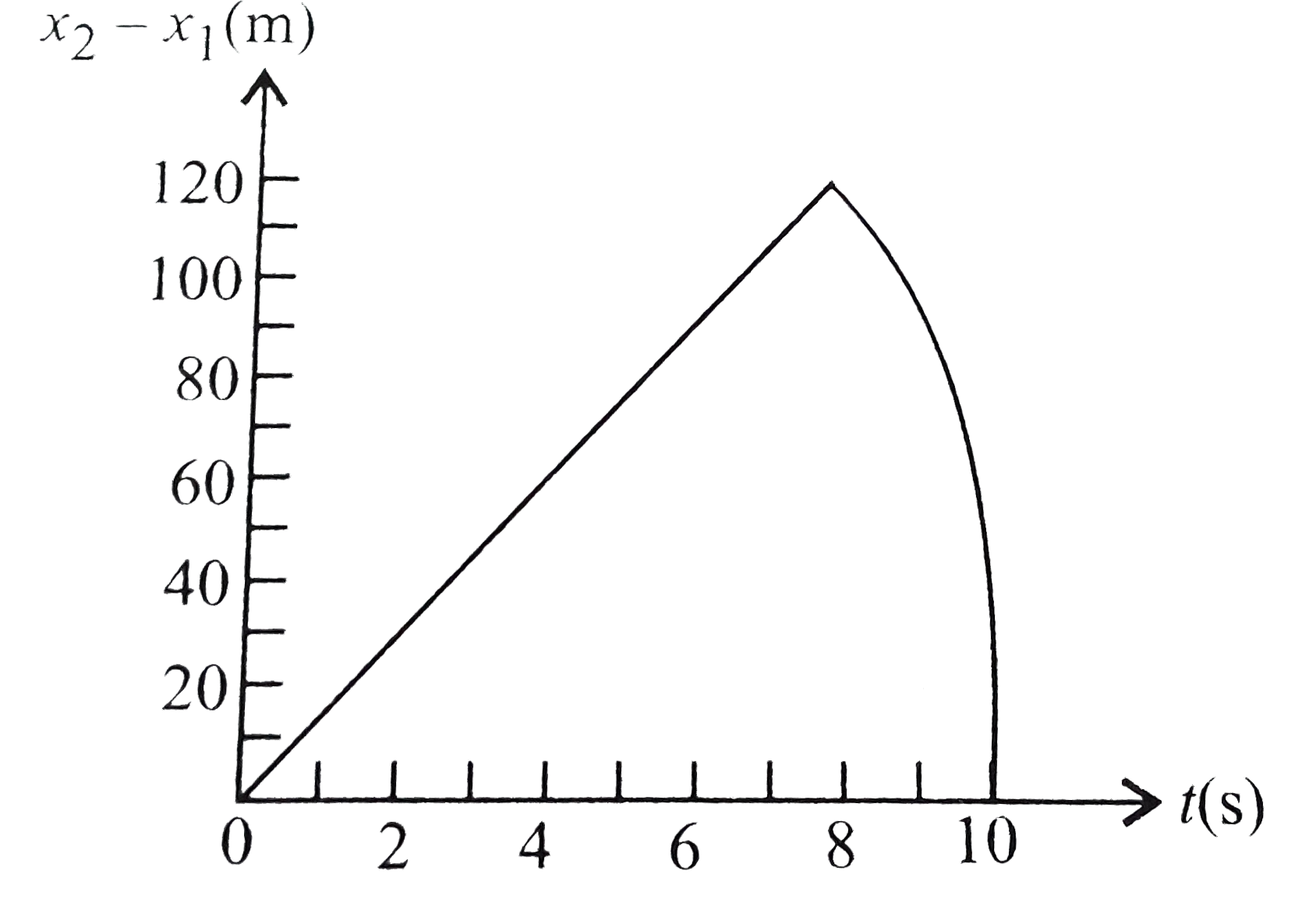
View Solution

