For four sine waves, moving on a string along positive x-direction, displacement distance curves (y-x curves) as shown at time t=0. in this right column, expression for y as function of distance x and time t for sinusoidal waves are given. All terms in the equation have their usual meanings. Correctly match y-x curves with corresponding equation.
A-P,B-Q,C-S,D-R
A-R,B-S,C-Q,D-P
A-R,B-P,C-S,D-Q
A-Q,B-R,C-P,D-S
The correct Answer is:C
Use x=0, t=0 for y and particle velocity δyδt
Life for (P), at x=0 and t=0, y=0 and particle velocity δyδt>0,
Therefore, it matches with (3) in column (II)
For (Q) in column (I): at x=0 and t=0, Y=A and δyδt=0. therefore, it matches with (I) in column (II) similarly all matches can be evaluated.
Similar Questions
A wave pulse is travelling on a string at 2m/s along positive x-directrion. Displacement y of the particle at x = 0 at any time t is given by
y=2t2+1 Find
Shape of the pulse at t = 0 and t = 1s.
View SolutionA wave propagates on a string in the positive x-direction at a velocity u. The shape of the string at t=t0 is given by g(x,t0)=Asin(xa) . Write the wave equation for a general time t.
View Solution
Knowledge Check
A long itudinal sine wave is travelling in air along positive x-direction. Displacement(s) of particles from their mean positions at a particular time t are shown in the figure. Choose the correct options for that instant only
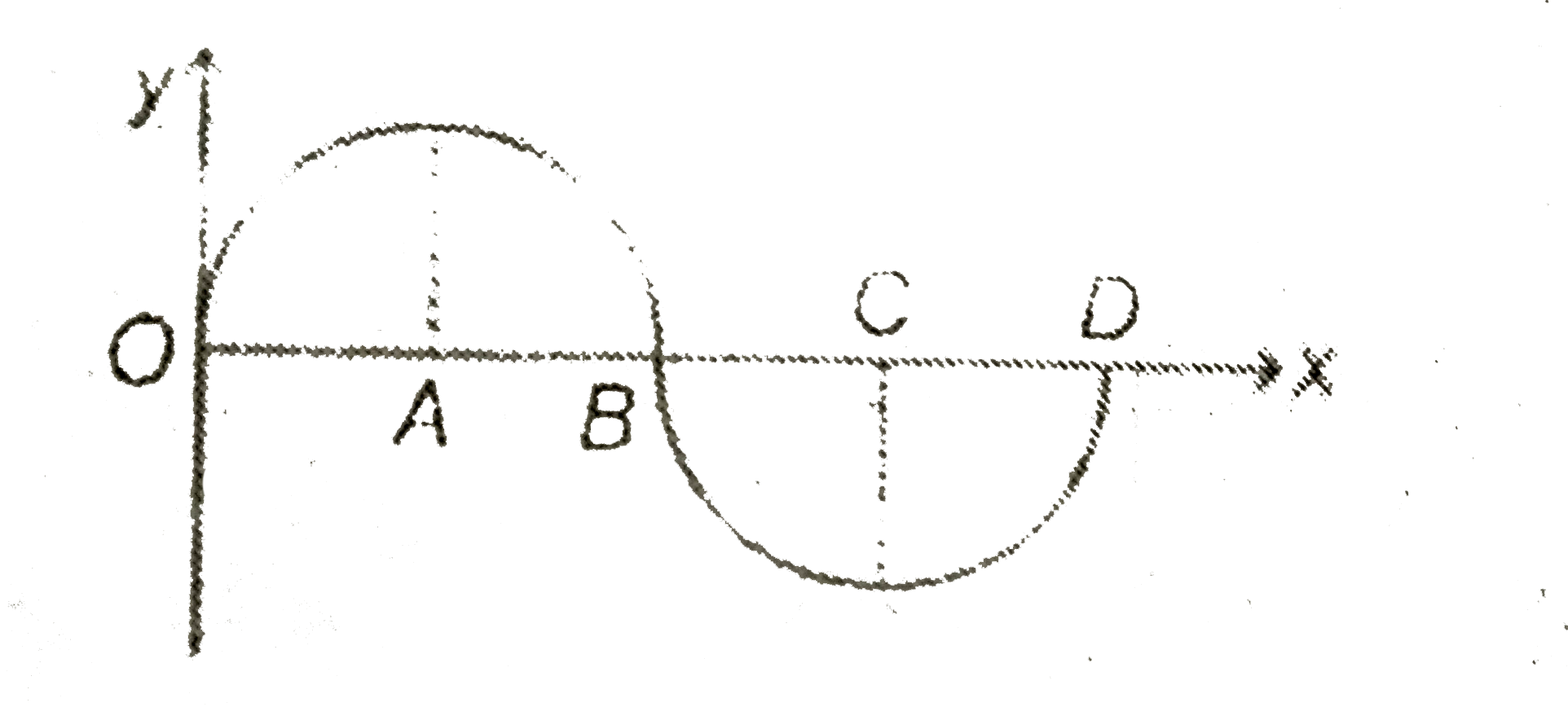AParticle located at C has zero velocity .BParticle located at C is equal to normal atmospheric directionCThe pressure at C is equal to normal atmospheric pressure .DParticles located near B are under compression.A wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
Aϕ=0Bϕ≡πCϕ=π/2Dϕ=3π/2A wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given byAg(x,t)=Asin[x−v(t−t0)]2a2Bg(x,t)=Asin[x+v(t−t0)]2a2Cg(x,t)=Asin[x−v(t+t0)]2a2Dg(x,t)=Asin[x+v(t+t0)]2a2
A wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(i) Expression of the function y = (x, t) i.e., displacement of a particle position x and time t.
View SolutionA sinusoidal wave having wavelength of 6m propagates along positive x direction on a string. The displacement (y) of a particle at x=2m varies with time (t) as shown in the graph
(a) Write the equation of the wave
(b) Draw y versus x graph for the wave at t=0
View Solution(i) A sinusoidal wave is travelling along positive x direction and the displacements at two positions x=0 and x=1m are given by y(0,t)=0.2cos(3πt) and y(1,t)=0.2cos(3πt+π8) Find all possible wavelength of the wave if it is known that wavelength is greater than 0.4 m.
(ii) A transverse sine wave of amplitude a=0.1cm is travelling along a string laid along the x-axis. The displacement (y) – time (t) graph of the string particle at x=0.1m is shown in first figure. The shape of the string at time t=0.1s is shown in second figure. At this time the particle at x=0.11m is having velocity in positive y direction write the equation of wave.
View SolutionThe sketch in the figure shows displacement time curve of a sinusoidal wave at x=8m. Taking velocity of wave v=6m/s along positive x−axis, write the equation the wave.
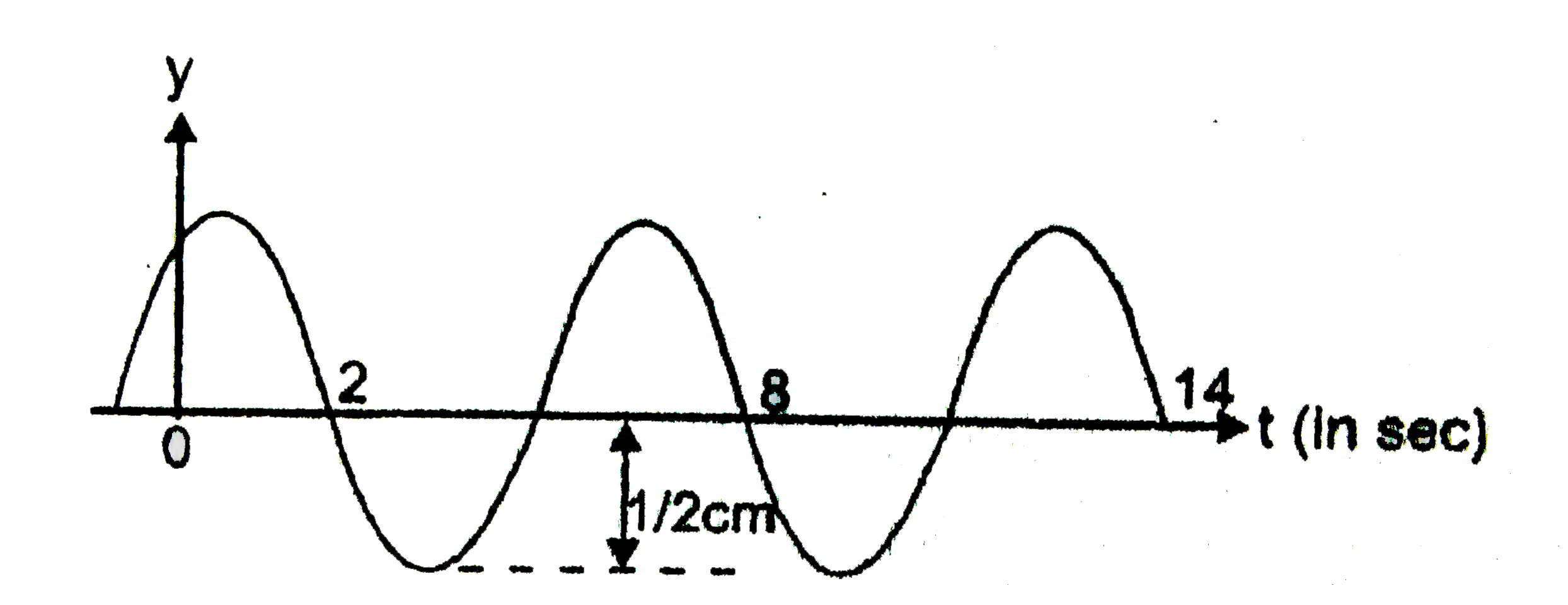
View SolutionA wave pulse is travelling along +x direction on a string at 2m/s. Displacement y (in cm ) of the parrticle at x=0 at any time t is given by 2/(t2+1). Find
(i) expression of the function y=(x,t),i.e., displacement of a particle at position x and time t.
Draw the shape of the pulse at t=0 and t=1 s.
View Solution