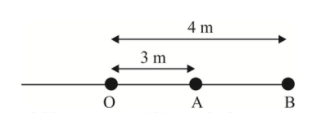
A particle is performing SHM about mean position O as shown in the figure given below. Its amplitude is 5 m and time period of oscillation is 4 s. The minimum time taken by the particle to move from point A to B is nearly
0.18 s
0.20s
0.15s
0.24s
The correct Answer is:A
The displacement equation of SHM is
x=Asinωt⇒sinωt=xA⇒ωt=sin−1(XA)
Substiuting the given values , we get
ωt1=sin−1(35)=37∘(37×π180)rad…….(i)
And ωt2=sin−1(45)=53∘=(53×π180)rad.....(ii)
Subracting eq.(i)from eq.(ii),we get
ω(t2−t1)=(53−37)π180
⇒t2−t1=1ω(53−37)π180=T2π(16)π180=8T180=8×4180=845=0.18s.
Similar Questions
A particle is performing SHM along x−axis with amplitude 4.0cm and time period 1.2s . What is the minimum time is deci− second taken by the particle to move from x=+2cmto x=+4cm and back again.
View SolutionA particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View Solution
Knowledge Check
The particle performing S.H.M., about mean position it has
Amaximum acceleration and maximum velocityBminimum acceleration and maximum velocityCmaximum acceleration and minimum velocityDminimum acceleration and minimum velocityA particle performing S.H.M. about their mean position with the equation of velocity is given by 4v2=25−x2, then the period of motion is
A2πBπC3πD4πA particle executes simple harmonic oscillation with an amplitudes a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
AT8BT12CT2DT4.
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
View SolutionA particle executes simple harmonic oscilliation with an amplitude a. The period of oscillations is T. The minimum time taken by the particle to travel half to the amplitude from the equlibrium position is
View SolutionA particle is performing a linear S.H.M about the mean position with the equation of velocity given by 4v2−25−x2. Then the period of motion is
View SolutionA particle starts with S.H.M. from the mean position as shown in the figure. Its amplitude is A and its time period is T. At any instant, its speed is half that of the maximum speed. What is the displacement of the particle at the that point?
View SolutionA particle performing S.H.M. about equilibrium position. Then the velocity of the particle is
View Solution
