A particle starts from a point P at a distance of A/2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is

x=Asin(2πTt+π6)
x=Asin(2πTt+5π6)
x=Acos(2πTt+π6)
x=Acos(2πTt+π3)
The correct Answer is:B, D
x=Asin(ωt+150∘)

=Asin(2πTt+5π6)
or x=Acos(ωt+60∘)
=Acos(2πTt+π3)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Comprehension
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Subjective
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle start form mean position and moves towards positive extreme as shown. Find the equation of the SHM. Amplitude of SHM is A.

View SolutionA particle starts from mean position and moves towards positive extreme as show below. Find the equation of the SHM, Amplitude of SHM is A.
_S01_003_Q01.png)
View Solution
Knowledge Check
A particle starts from a point P at a distance of A/2 from the mean position O& travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of motion of particle is :
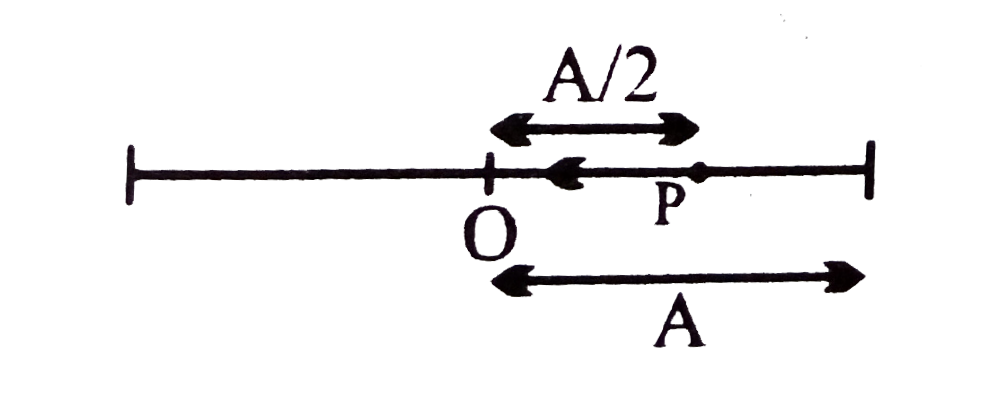 AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3)
AX=Asin(2πTt+π6)BX=Asin(2πTt+5π6)CX=Acos(2πTt+π6)DX=Acos(2πTt+π3)A particle executes SHM of amplitude A. At what distance from the mean position is its KE equal to its PE ?
A0.71 AB0.61 AC0.65 AD0.8 AThe amplitude of a particle executing SHM about O is 10cm. Then
Awhen the KE is 0.64 times of its maximumKE, its displacement is 6cm from OBits speed is half the maximum speed when its displacement is half the maximum displacementCBoth (a) and (b) are correctDBoth (a) and (b) are wrong
The period of a particle executing SHM is T. There is a point P at a distance 'x' from the mean position 'O'. When the particle passes P towards OP, it has speed v. Find the time in which it returns to P again.
View SolutionThe figure shows the displacement-time graph of a particle executing SHM. If the time period of oscillation is 2s, then the equation of motion is given by
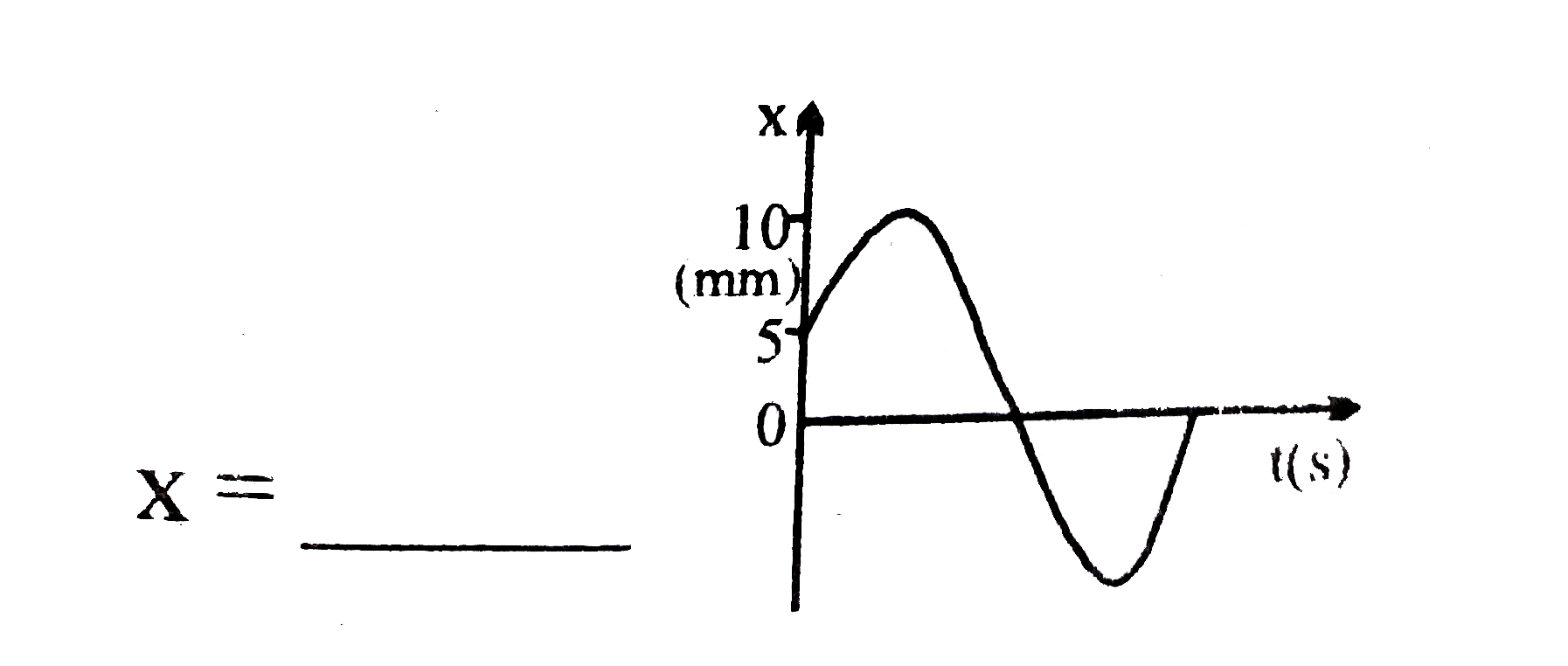
View SolutionThe displacement from mean position of a particle in SHM at 3 seconds is √3 /2 of the amplitude. Its time period will be :
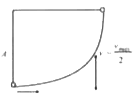
View SolutionA particle starts with S.H.M. from the mean position as shown in the figure. Its amplitude is A and its time period is T. At any instant, its speed is half that of the maximum speed. What is the displacement of the particle at the that point?
View SolutionThe displacement (from intial position) of a particle executing SHM with amplitude A in half the time period is always
View Solution