The displacement from mean position of a particle in SHM at 3 seconds is √3 /2 of the amplitude. Its time period will be :
18 sec.
6√3sec.
9sec.
3√3sec.
The correct Answer is:A
To solve the problem, we need to determine the time period of the simple harmonic motion (SHM) given that the displacement at 3 seconds is √32 of the amplitude.
Step 1: Understand the displacement in SHM
The displacement Y of a particle in SHM can be expressed as:
Y=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
Step 2: Substitute the given values
According to the problem, at t=3 seconds, the displacement Y is given as:
Y=√32A
Substituting this into the SHM equation, we have:
√32A=Asin(ω⋅3)
Step 3: Simplify the equation
We can divide both sides of the equation by A (assuming A≠0):
√32=sin(ω⋅3)
Step 4: Find the angle corresponding to the sine value
From trigonometry, we know that:
sin(π3)=√32
Thus, we can equate:
ω⋅3=π3
Step 5: Solve for ω
Now, we can solve for ω:
ω=π3⋅3=π9
Step 6: Relate angular frequency to time period
The angular frequency ω is related to the time period T by the formula:
ω=2πT
Substituting our value of ω:
π9=2πT
Step 7: Solve for the time period T
Cross-multiplying gives:
πT=18π
Dividing both sides by π:
T=18
Thus, the time period T of the simple harmonic motion is 18 seconds.
---
The displacement Y of a particle in SHM can be expressed as:
Y=Asin(ωt)
where A is the amplitude and ω is the angular frequency.
According to the problem, at t=3 seconds, the displacement Y is given as:
Y=√32A
Substituting this into the SHM equation, we have:
√32A=Asin(ω⋅3)
We can divide both sides of the equation by A (assuming A≠0):
√32=sin(ω⋅3)
From trigonometry, we know that:
sin(π3)=√32
Thus, we can equate:
ω⋅3=π3
Now, we can solve for ω:
ω=π3⋅3=π9
The angular frequency ω is related to the time period T by the formula:
ω=2πT
Substituting our value of ω:
π9=2πT
Cross-multiplying gives:
πT=18π
Dividing both sides by π:
T=18
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - A Previous Year Problems | NEET
Explore 24 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
Explore 23 Videos
- SIMPLE HARMONIC MOTIONBook:MOTIONChapter:SIMPLE HARMONIC MOTIONExercise:EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum
Explore 6 Videos
- SEMI CONDUCTOR AND LOGIC GATESBook:MOTIONChapter:SEMI CONDUCTOR AND LOGIC GATESExercise:EXERCISE 3
Explore 34 Videos
- SIMPLE HARONIC MOTION Book:MOTIONChapter:SIMPLE HARONIC MOTION Exercise:EXERCISE -4 (Leve-II) [ JEE 2011]
Explore 11 Videos
Similar Questions
The shortest distance travelled by a particle executing SHM from mean position in 2 s is equal to (√3/2) times its amplitude. Determine its time period.
View SolutionA particle is performing SHM aong x-axis,such that its velocity is v1 when its displacement from mean position is x1 and v2 when its displacement from mean position is x2.Time period of oscillation is
View Solution
Knowledge Check
The displacement (from intial position) of a particle executing SHM with amplitude A in half the time period is always
AzeroBACanything from 0 to ADanything from 0 to 2AThe following graph shows the displacement of the bob from its mean position versus time . The time period and the amplitude of the bob are :
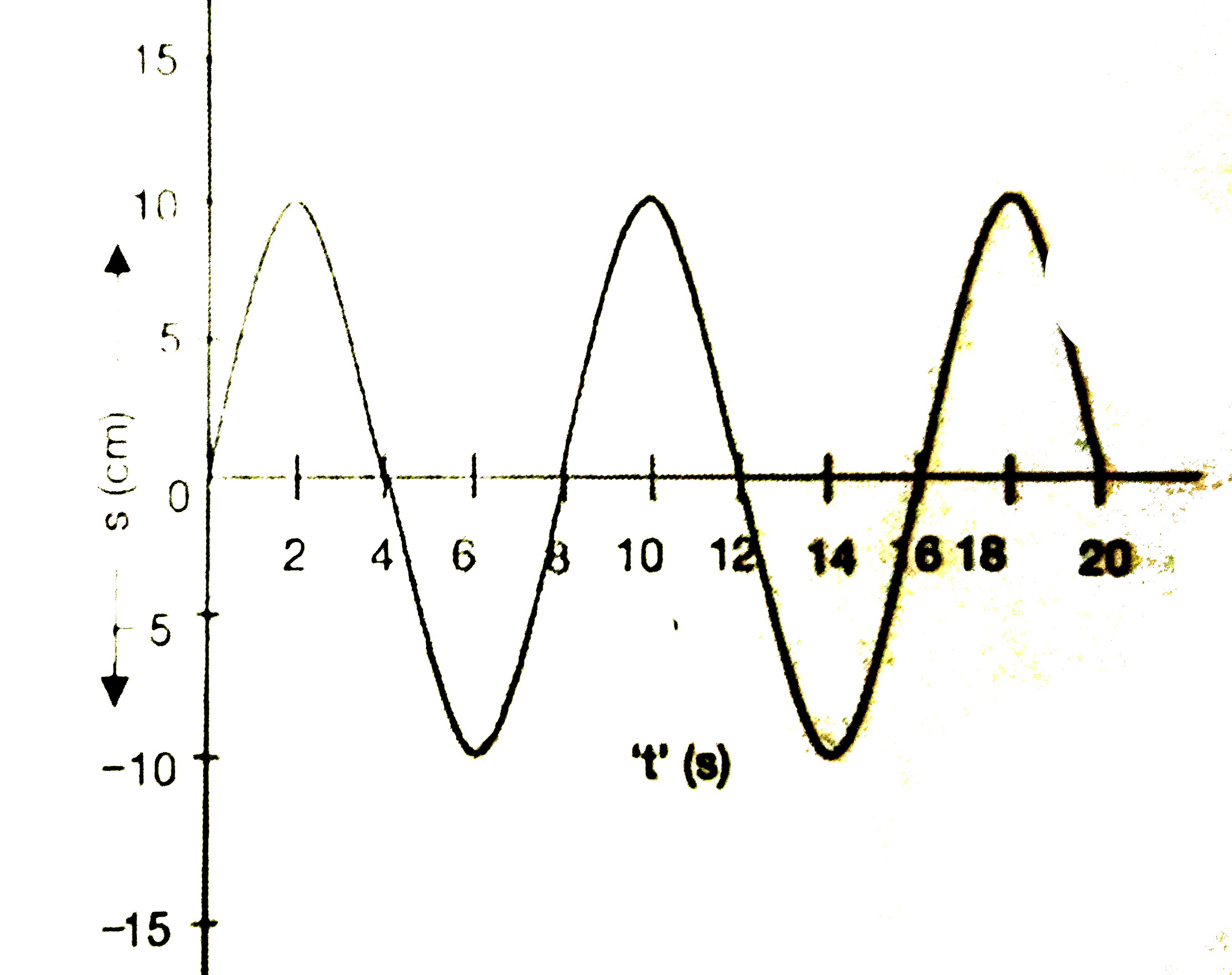 A4s , 5 cmB8s , 10 cmC4s , 10 cmD8s , 5 cm
A4s , 5 cmB8s , 10 cmC4s , 10 cmD8s , 5 cmA particle executing SHM has a velocity of 2 ms−1 when its displacement from mean position is 1 cm and a velocity of 1ms−1 when its displacement is 2 cm. Its amplitude of oscillationis
A5 cmB√5cmC3 cmD√7cm
A particle executies linear simple harmonic motion with an amplitude 3cm .When the particle is at 2cm from the mean position , the magnitude of its velocity is equal to that of acceleration .The its time period in seconds is
View SolutionThe period of oscillation of a particle in SHM is 4sec and its amplitude of vibration is 4cm. The distance of the particle 0.5s after passsing the mean position is
View SolutionAt a particular position the velocity of a particle in SHM with amplitude a is √3/2 that at its mean position. In this position, its displacement is :
View SolutionAmplitude of oscillation of a particle that executes SHM is 2cm. Its displacement from its mean position in a time equal to 1/6th of its time period is
View SolutionA particle executes linear simple harmonic motion with an amplitude of 3cm. When the particle is at 2cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then, its time period in seconds is
View Solution
