A solid sphere of radius is cut out of a solid sphere of radius such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was . If a particle of mass is placed at a distance from the centre of the cavity, then what is the gravitational attraction on the mass ?

The correct Answer is:D
Let mass of the cavity = M
Density of the sphere
Mass of the cavity out = M
Similar Questions
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View Solution
Knowledge Check
The radius of gyration of a solid sphere of radius R about a certain axis is also equal to R. If r is the distance between the axis and the centre of the sphere, then r is equal to
ARB0.5RC√0.6RD√0.3RThe radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4rA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
A11GMmR2B14GMmR2CGMm2R2DGMmR2
A uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View SolutionA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
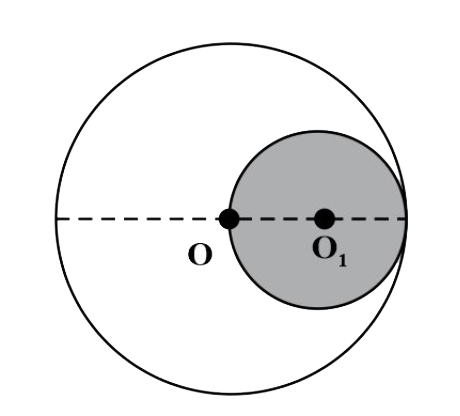
View SolutionThe moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionA spherical hole is made in a solid sphere of radius R. The mass of the sphere before hollowing was M. The gravitational field at the centre of the hole due to the remaining mass is

View Solution