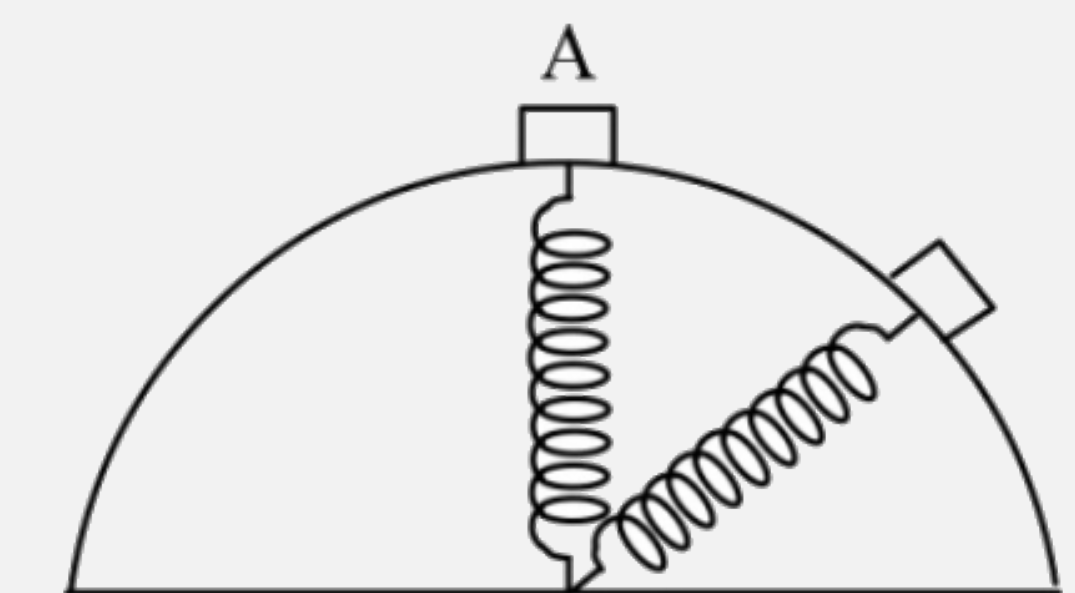
A smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R/4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60∘ with the vertical. The spring constant K=mg/R. Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.

The correct Answer is:(i) 8 (ii) 0.375
The free body diagram of the ring is shown in the figure. The force acting on the ring are
(A) the weight mg acting vertically downwards,
(B) Normal force N by the wire track. Normal force on the ring could be either radially outwards or radially inwards depending on whether the ring presses against the inner surface or outer surface of the track. Ascertain whether normal force is inwards or outward assume that, to being with, it is inwards then from ∑→F=m→a find the value of normal force, if it is +ve it is inward and if it is ve, it is outwards.
(C) Force of the spring kx. In the physical situation given the spring is extended, it will pull the ring. So the spring force kx is along the spring towards O.
Length of the spring in the position shown = R.
(CP=CO=R,∠COP=∠COP=∠OPC=60∘,ΔCOP is equilateral)
Change in length of the spring =R−(43)R=(R4)kx=(mgR)(R4)=mg4)
Now from Ft=mat(mg4)cos30∘+mgcos30∘=mat⇒at=5√38g
Now consider in radial direction n+kxcos60∘=mgcos60∘
⇒N=mgcos60∘−kxcos60∘ ⇒N=mg2−[mg4]12=3mg8

Similar Questions
A bead of mass m can slide without friction on a fixed circular horizontal ring of radius 3R having a centre at the point C. The bead is attached to one of the ends of spring of spring constant k. Natural length of spring is R and the other end of the spring is R and the other end of the spring is fixed at point O as shown in the figure. If the bead is released from position A, then the kinetic energy of the bead when it reaches point B is
View SolutionA bead of mass m can slide without friction along a vertical ring of radius R. One end of a spring of force constant k=3mgR is connected to the bead and the other end is fixed at the centre of the ring. Initially, the bead is at the point A and due to a small push it starts sliding down the ring. If the bead momentarily loses contact with the ring at the instant when the spring makes an angle 60∘ with the vertical, then the natural length of the spring is
View Solutionएक चिकने अर्धवृत्ताकार आकृति की R त्रिज्या वाली तार की ऊर्ध्व तल में स्थित है। लीक के निम्नतम बिन्दु O पर 3R4 स्वाभाविक लम्बाई की एक भारहीन स्प्रिंग का एक सीरा जुड़ा है। स्प्रिंग का दूसरा सीरा m द्रव्यमान के एक छल्ले बिन्दु P पर स्थितरावस्था में है तब स्प्रिंग उर्ध्व से 60∘ का कोण बनाती है। स्प्रिंग नियतांक k=mg/R है। जब छल्ले को मुक्त किया जाता है तब
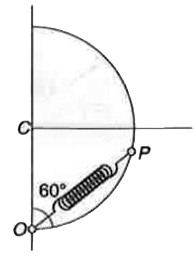
(a) छल्ले का बल निर्देशांक आरेख बनाइये।
(b) छल्ले के स्पर्शरेखीय त्वरण तथा अभिलम्ब प्रतिक्रिया के मान ज्ञात कीजिए।
View SolutionThe figure shows a smooth track, a part of which is a circle of radiur R. A block ofmas m is pushed against a spring of spring constant K fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal?

View SolutionA bead of mass m is attached to one end of a spring of natural length R and spring constant K=((sqrt(3)+1)mg)/(R ) . The other end of the spring is fixed at a point A on a smooth vertical ring of radius R as shown in fig. The normal reaction at B just after it is released to move is
View SolutionA smooth semicircular wire-track of radius R is fixed in a vertical plane. One end of a massless spring of natural length 3R//4 is attached to the lowest point O of the wire-track. A small ring of mass m, which can slide on the track, is attached to the other end of the spring. The ring is held staionary at point P such that the spring makes an angle of 60^@ with the vertical. The spring constant K=mg//R . Consider the instant when the ring is released, and (i) draw the free body diagram of the ring, (ii) determine the tangential acceleration of the ring and the normal reaction.
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.

View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that /_OCA=60^@ , C being the centre of the ring. The natural length of the spring is also equal to r=20cm . After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (i n xx 10^2Nm^-1) of the spring.
View Solution