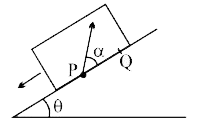
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

The correct Answer is:(3.75ˆi+6.25gˆj)m/s
Let after time ‘t’ the stone hits the object and be the angle which the velocity vector makes with horizontal
From question, we have following information Vertical displacement of stone is 1.25 m
Using sy=uyt+12ayt2
Therefore 1.25 =(usinθ)t−12>2or(usinθ)t=1.25+5t2...(i)
Horizontal displacement of stone = 3 + displacement of object A.
Therefore (ucosθ)t=3+12at2
We have a=1.5m/s2,Hence (ucosθ)t=3+0.75t2.....(ii)
Horizontal component of velocity (of stone) = vertical component (because velocity vector is inclined at 45∘ with horizontal).
Therefore (ucosθ)=>−(usinθ)........(iii)
The right-hand side is written because the stone is in its downward motion. Therefore >>usinθ
Multiplying equation (iii) with t can write. (ucosθ)t+(usinθ)t=10t2......(iv)
Now doing (iv)-[(iii)+(i)]
It gives 4.25t2−4.25ort=1s Substituting t=1 s in (i) and (ii) we get
usinθ=6.25m/sorvy=6.25manducosθ=3.75m/sorux=3.75m/s
Now, we can write u=uxˆi+uyˆioru=(3.75ˆi+6.25ˆj)m/s 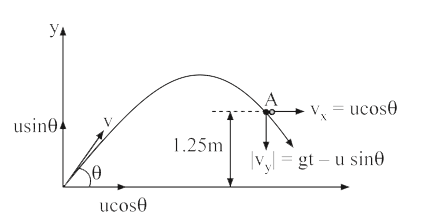
Similar Questions
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solutionθ नत कोण वाले घर्षण रहित तल पर एक बड़ा भारी बॉक्स फिसल रहा है। बाक्स के तल पर स्थित बिन्दु P से बॉक्स के भीतर एक कण प्रक्षेपित किया जाता है। कण की बॉक्स के सापेक्ष प्रारम्भिक वेग u है तथा प्रक्षेपण की दिशा तल से चित्रानुसार α है।
(a) बॉक्स में नत के अनुदशि प्रक्षेपण बिन्दु P से Q की दूरी ज्ञात करो जहाँ कण टकराता है। (कण बॉक्स में और कही नही टकराता एवं वायु प्रतिरोध नगण्य है
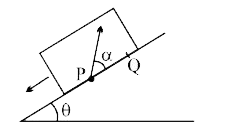
View Solutionθ नत कोण वाले घर्षण रहित तल पर एक बड़ा भारी बॉक्स फिसल रहा है। बाक्स के तल पर स्थित बिन्दु P से बॉक्स के भीतर एक कण प्रक्षेपित किया जाता है। कण की बॉक्स के सापेक्ष प्रारम्भिक वेग u है तथा प्रक्षेपण की दिशा तल से चित्रानुसार α है।
यदि धरातल पर खड़े प्रेक्षक के लिये कण का क्षैतिज विस्थापन शून्य हो तो जब कण प्रक्षेपित किया गया था तब बॉक्स की धरातल के सापेक्ष चाल क्या थी।
View SolutionA rectangular box is sliding on a smooth inclined plane of inclination α as shown in the figure. At t = 0, the box starts to move on the inclined plane. A bolt starts to fall from point A. Find the time after which bolt strikes the bottom surface of the box.
View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .

View SolutionA large box is moving on a horizontal floor with constant acceleration a=g. A particle is projected inside box with velocity u and angle θ with horizontal from box frame. For the given u, the value of θ for which horizontal range inside he box will be maximum is

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View SolutionA large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .

View Solution
