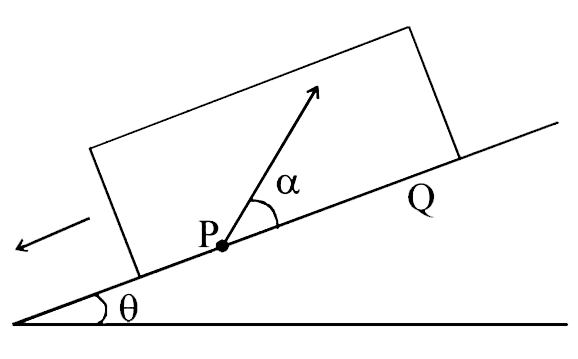
A large , heavy box is sliding without friction down a smooth plane of inclination θ . From a point P on the bottom of the box , a particle is projected inside the box . The initial speed of the particle with respect to the box is u , and the direction of projection makes an angle α with the bottom as shown in Figure .
(a) Find the distance along the bottom of the box between the point of projection p and the point Q where the particle lands . ( Assume that the particle does not hit any other surface of the box . Neglect air resistance .)
(b) If the horizontal displacement of the particle as seen by an observer on the ground is zero , find the speed of the box with respect to the ground at the instant when particle was projected .
u2sin2αgcosθ
u2cos2αgcosθ
u2sin2α2gcosθ
u2sin2α2gsinθ
The correct Answer is:A
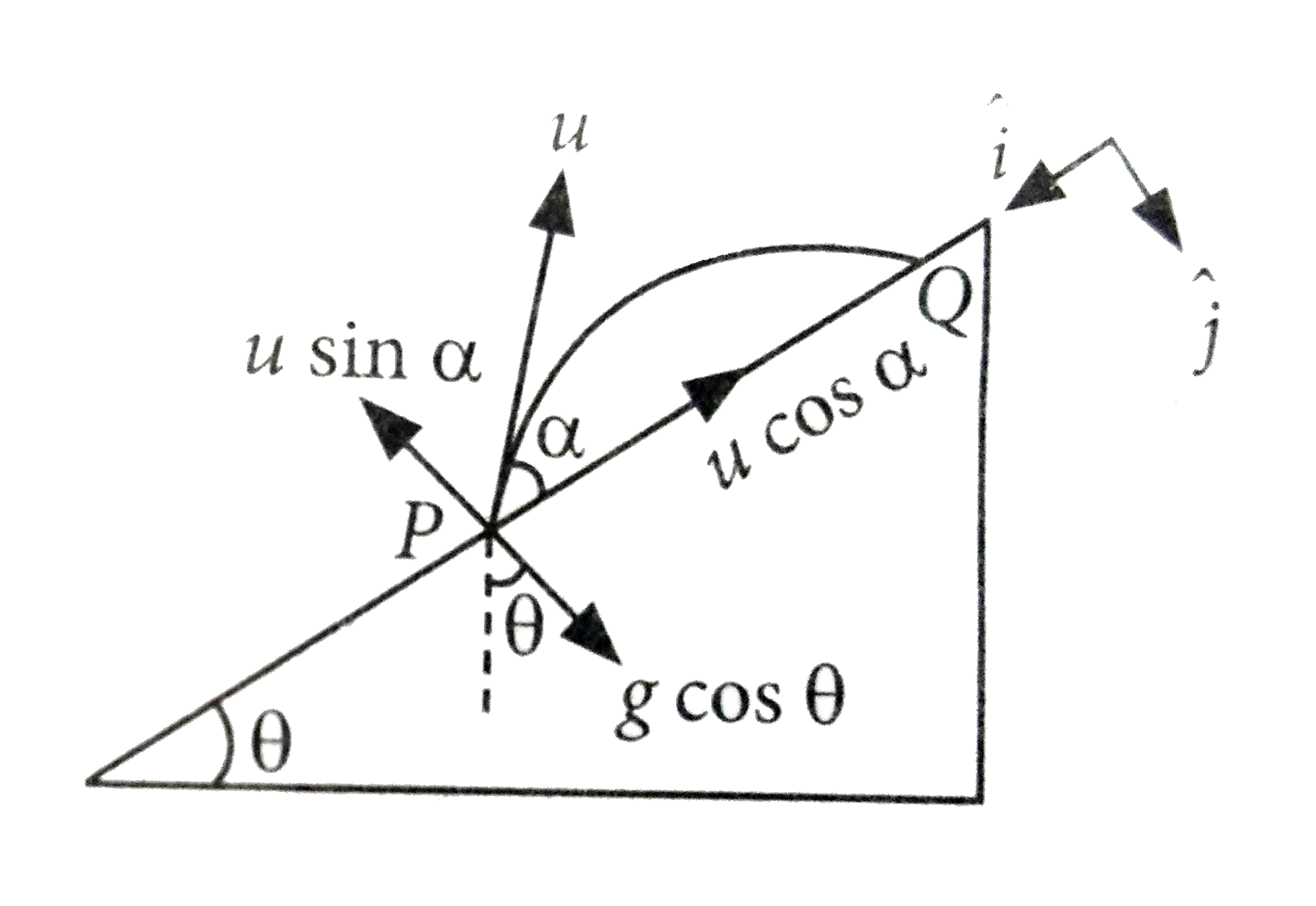
Take the x-axis along incline and y-axis perpendicular to the plane. ∴ Acceleration of particle =gsinθˆi+gcosθˆj and acceleration of block =gsinθˆi
∴ Acceleration of particle with respect to block
= acceleration of particle -acceleration of block
=(gsinθˆi+gcosθˆj)−(gsinθ)ˆi=gcosθˆj
Now motion of particle with respect to block will be a projectile as shown.
The only difference is, g will be replaced by g cos θ
∴PQ=Range(R)=u2sin2αgcosθ
PQ=u2sin2αgcosθ
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - NCERT Exemplar
10 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Miscellaneous Questions
14 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
Similar Questions
Knowledge Check
in the question number 4, if the horizontal displacement of the particle as seen by an observer on the ground is zero, the speed of the box with respect to the ground at the instant when particle was projected is
AucosαBusinαcosθCucos(α+θ)cosθDusinθsinαcosθ
A particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle of mass m is projected with speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
View SolutionA particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10ms2)

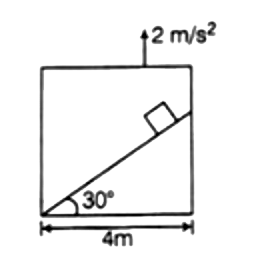
View SolutionA particle slides down on a smooth incline of inclination 30∘, fixed in an elevator going up with an acceleration 2m/s2. The box of incline has width 4m. The time taken by the particle to reach the bottom will be
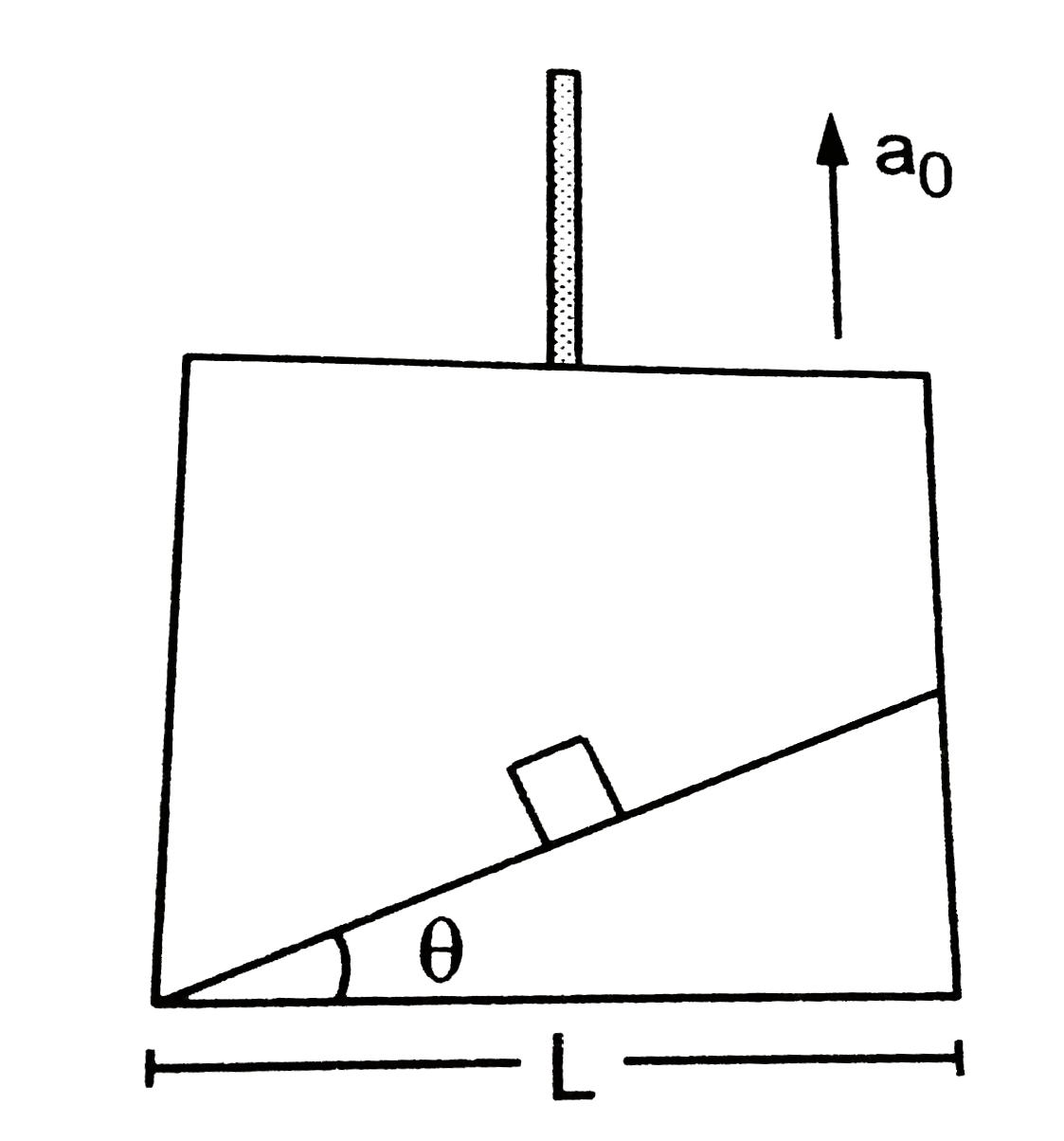
View SolutionA particle slides down a smooth inclined plane of elevation θ fixed in an elevator going up with an accelerationa0. The base of the incline has a length L.Find the time taken by the particle to reach the bottom.
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View SolutionA particle of mass m is projected from the ground with an initial speed u at an angle α. Find the magnitude of its angular momentum at the highest point of its trajector about the point of projection.
View Solution

 .
.