A belt moves over two pulleys A and B as shown in the figure. The pulleys are mounted on two fixed horizontal axles. Radii of the pulleys A and B are 50 cm and 80 cm respectively. Pulley A is driven at constant angular acceleration of 0.8 rad/s2 unitl pulley B acquries an angular velocity of 10 rad/s. The belt does not slide on either of the pulleys.
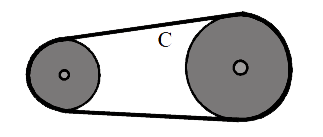
(a)Find the acceleration of a point C on the belt and angular acceleration of the pulley B.
(b) How long does it take for the pulley B to acquire an angular velocity of 10 rad/s ?
Since the belt does not slide on the pulleys, magnitudes of velocity and acceleration of any point on the belt are same as that of any point on the peridhery of either of the two pulleys.
→aT=→α×→r ac=αc=αArA=αBrB
Substituting rA=0.5m,rB=0.8 m and aA=0.8rad/s2
we have ac=0.4m/s2 and
αB=acrB=αArBrB=0.5rad/s2
we have ac=0.4m/s2 and αB=acrB=αArArB=0.5rad/s2
∵ω+ω0αt⇒t=ωB−ωB0αB
Substituting WBo0,ωB=10 rad/s and
αB=0.5rad/s2, we have t = 20 s
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 1
90 Videos
- ROTATIONAL MOTION BOOK - MOTIONCHAPTER - ROTATIONAL MOTION EXERCISE - Exercise - 2
40 Videos
- RAY OPTICSBOOK - MOTIONCHAPTER - RAY OPTICSEXERCISE - Exercise-4
38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
Similar Questions
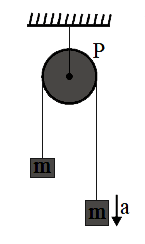
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
View Solution
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.
View Solution
Knowledge Check
Angular acceleration of the cylinder C shows in the figure is (all strings and the pulley are ideal)
 A2g3RB2g5RC2gRDg2R
A2g3RB2g5RC2gRDg2RAcceleration of pulleys and blocks are as shown in the figure. All pulleys & strings are massless & frictionless magnitude of aA and aB are :
 .AaA=0,aB=7BaA=0,aB=5CaA=0,aB=12DaA=5,aB=7
.AaA=0,aB=7BaA=0,aB=5CaA=0,aB=12DaA=5,aB=7In the arrangement shown, the pulleys and the string are ideal. The acceleration of block B is.
 Ag/5Bg/2C2g/5D2g/3
Ag/5Bg/2C2g/5D2g/3
Calculate the accelerations of the pulleys B and C and the tension in the string passing over the pulley A of the figure Figure 5.22.
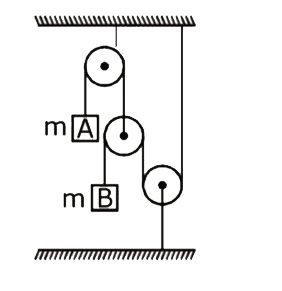
View SolutionIn the arrangement shown, the pulleys and the strings are ideal.The acceleration of the block B is
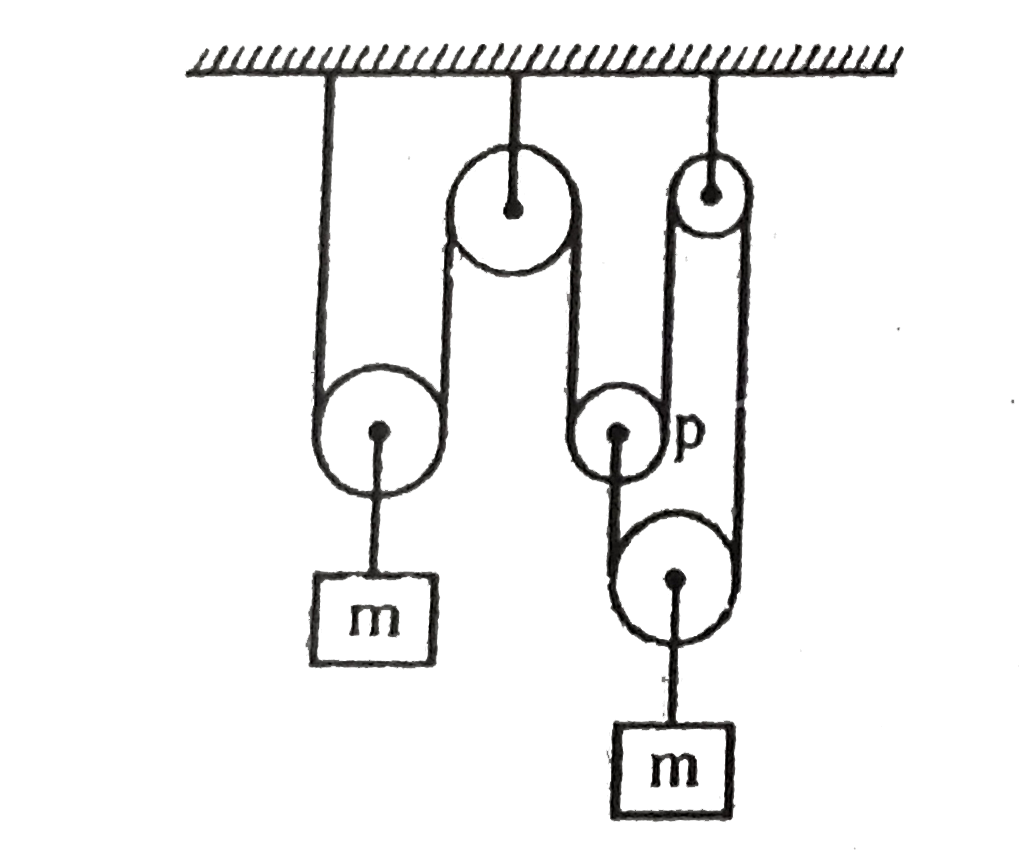
View SolutionAll pulleys are massless The string is light and inextensible Find acceleration of centre of pulley 'p'∈m/s2
View SolutionIf friction between pulley and string is sufficient to allow pure rolling then acceleration of pulley ‘A’ will be –
View SolutionIn the arrangement shown, the pulleys are smooth and the strings are inextensible. The acceleration of block B is :
View Solution
