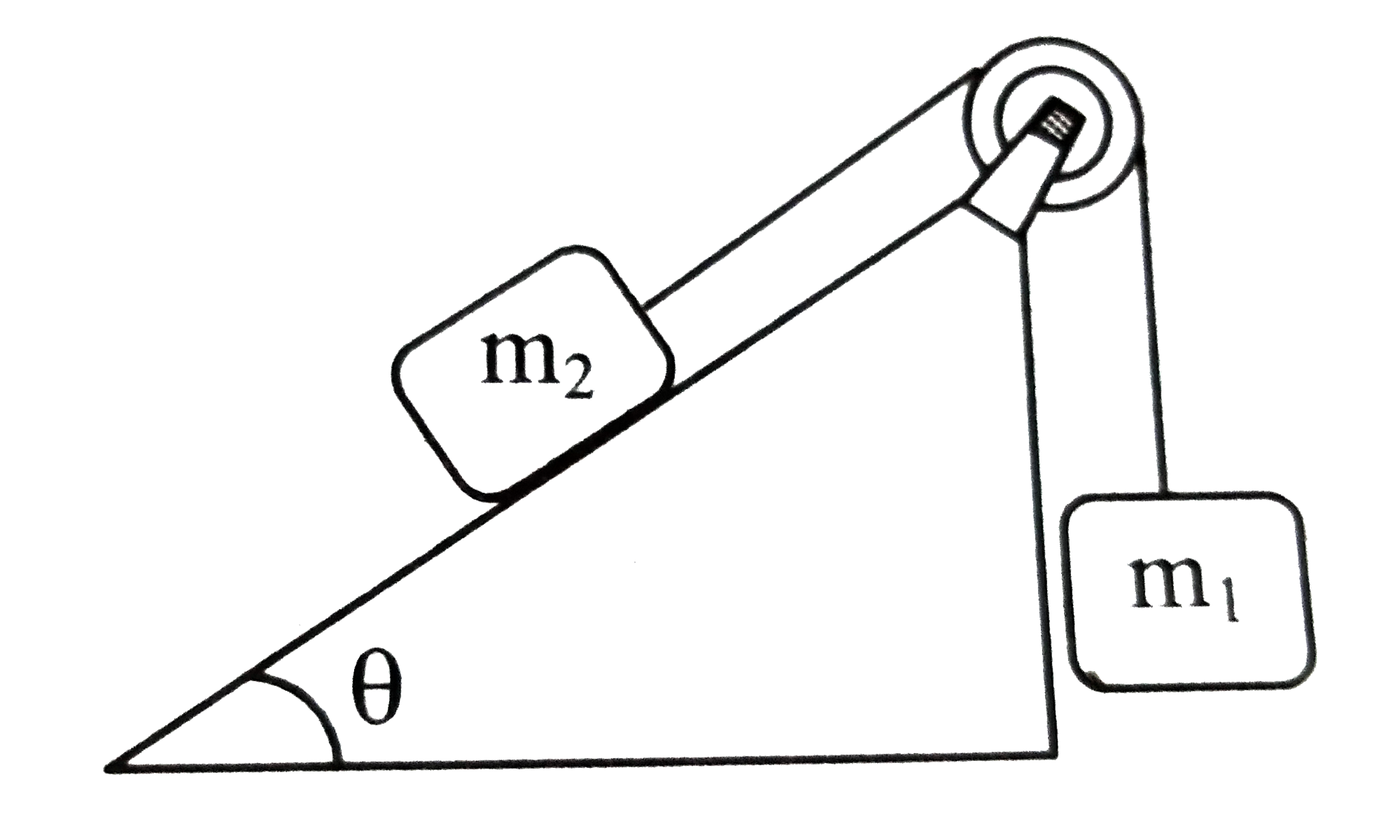
In the figure shown, the string and pulley are massless. The inclined plane is fixed and has coefficients of friction μs=0.25 and μk=0.2 . Consider two cases:
Case I : m1=2kgm2=1.5kgθ=37∘,Case II:m1=3kgm2=2kgθ=53∘
Take g=10m/s2,sin37∘=35,sin53∘=45
In case I, both blocks are in equilibrium
In case I, friction on is 3 N, acting down the plane
In case II, both blocks are in equilibrium
In case II, friction on m1 is 3.6 N, acting up the plane
The correct Answer is:abc
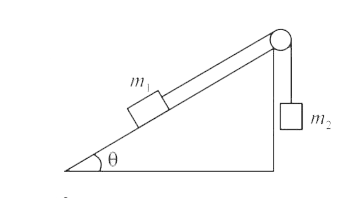
Assuming equilibrium T=m2g
Taking friction up the plane , T+f=m1gsinθ and N=mgcosθ
put f=μsN to get minimum allowed value of m2m2≥m1sinθ−μm1cosθ
reverser direction of friction to get maximum allowed value of m2m2≤m1sinθμm1cosθ
→ again m2 is in the right range → static friction acts as m2<m1sinθ friction acts up the plane
→T+F=m1gsinθ→T+F=m1gsinθ−T=m1gsinθ−m2g=24−20=4N
Similar Questions
Knowledge Check
In fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the stringA1207NB2407NC1307NDNone of theseIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 isA407ms−2B307ms−2C207ms−2D√17g7ms−2In fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 isA407ms−2B307ms−2C207ms−2DNone of these
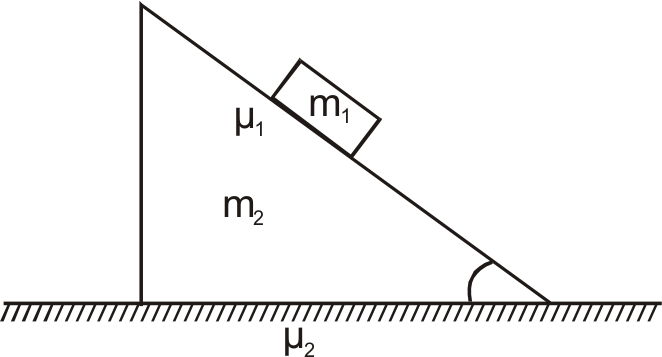
The block of mass m1 is placed on a wedge of an angle θ, as shown. The block is moving over the inclined surface of the wedge. Friction coefficient between the block and the wedge is μ1, whereas it is μ2 between the wedge and the horizontal surface. if μ1=12,θ=45∘,m1=4kg,m2=5kg and g=10m/s2, find minimum value of μ2 so that the wedge remains stationary on the surface. express your answer in multiple of 10−3
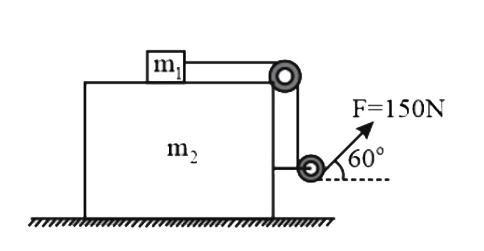
View SolutionIn the arrangement shown in the figure, friction exists only between the two blocks, A and B. The coefficient of static friction μs=0.6 and coefficient of kinetic friction μk=0.4, the masses of the blocks A and B are m1=20kg and m2=30kg, respectively. Find the acceleration (in ms−2) of m1, if a force F=150N is applied, as shown in the figure. [Assume that string and pulleys are massless]
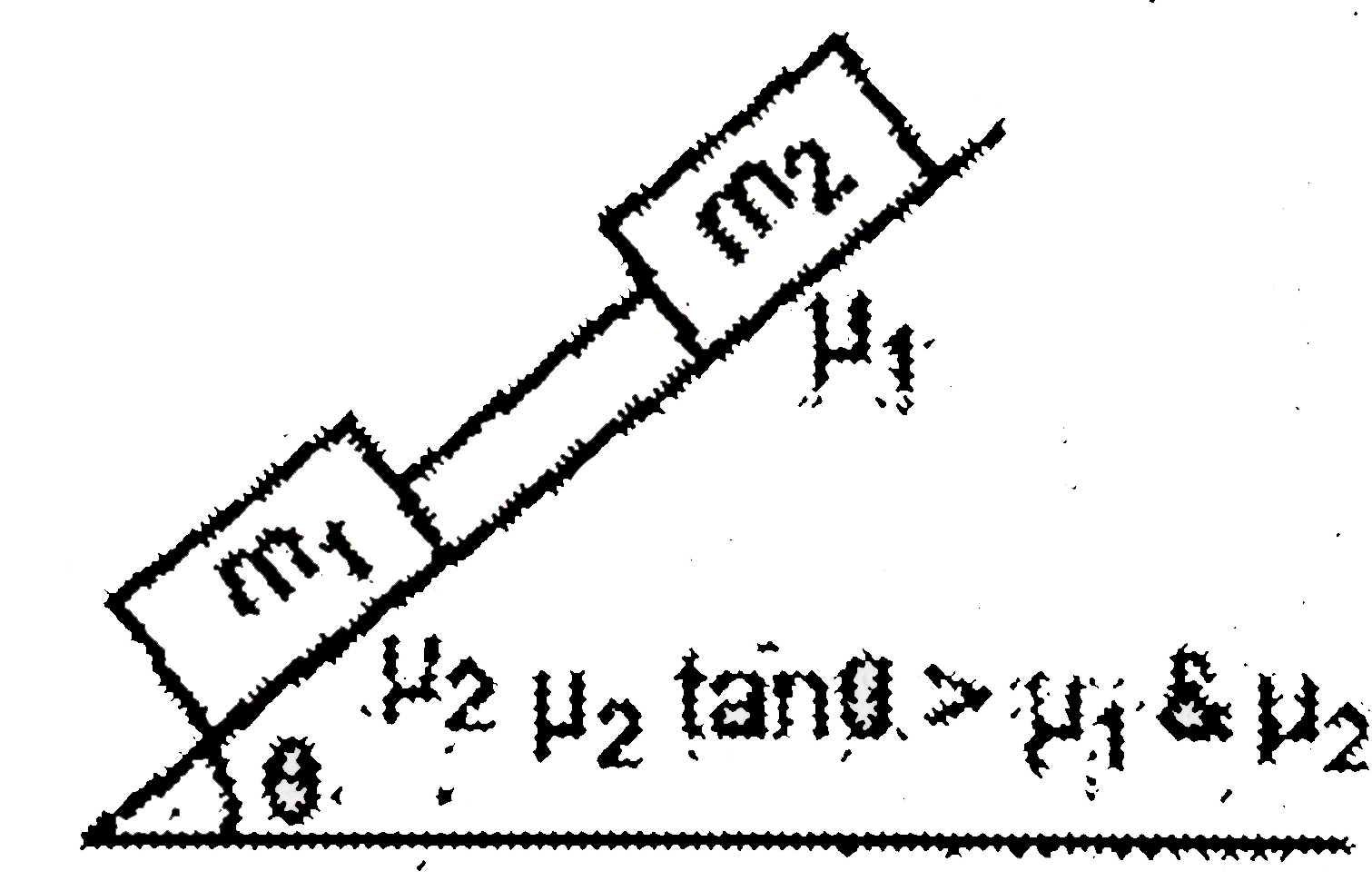
View SolutionTwo blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between m1 and inclined plane is μ1 & that betweeb m2 & the inclined is μ2. Then :
View SolutionTwo masses m1 and m2 which are connected with a light string, are placed over a frictionless pulley. This set up is placed over a weighing machine, as shown. Three combination of mass m1 and m2 are used, in first case m1=6kg and m2=2kg, in seconds case m1=5kg and m2=3kg and in third case m1=4kg and m2=4kg. masses are held stationary initially and then released. if the reading of the weighing machine after the release in three cases are W1,W2 and W3 respectively then:
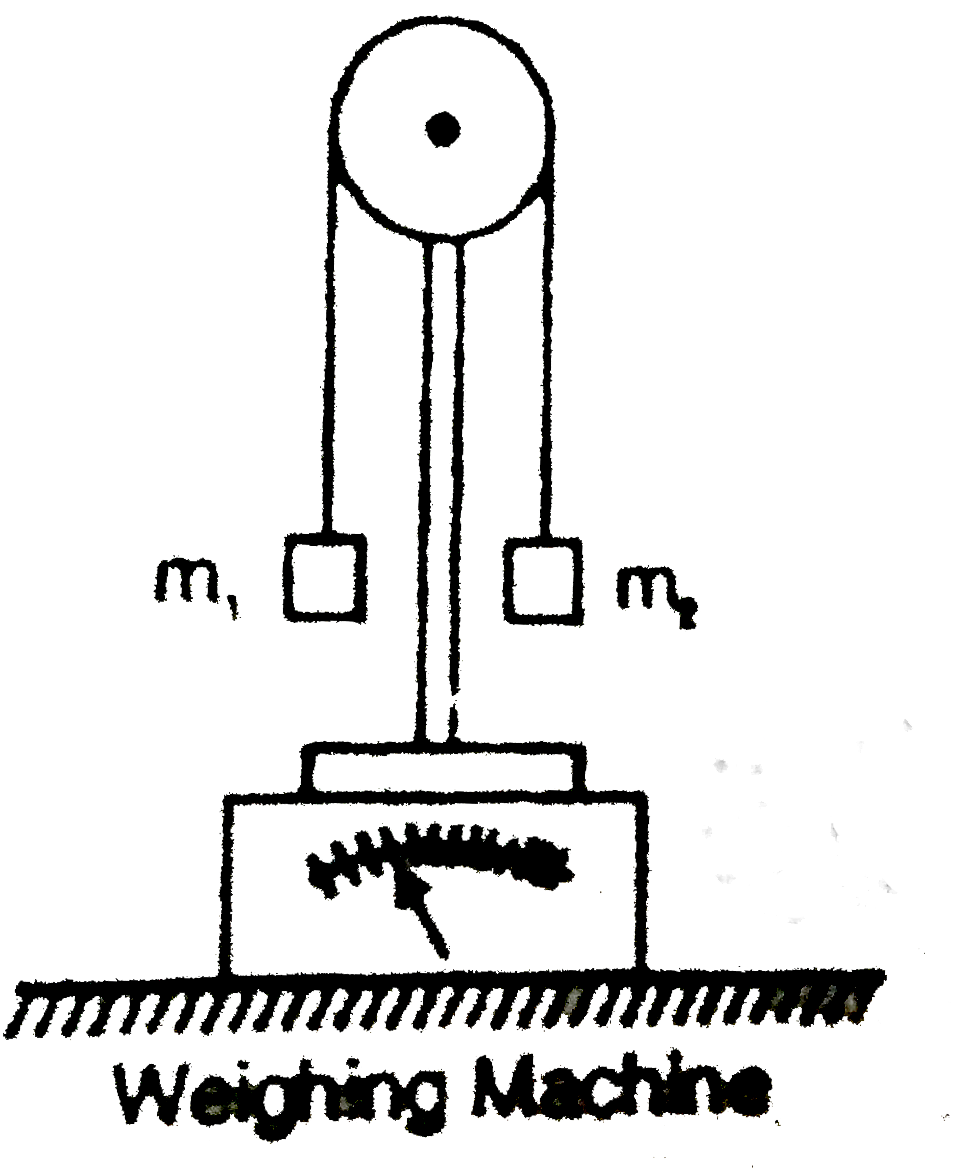
View SolutionIn the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?

View Solution