Two masses m1 and m2 are attached to the ends of a massless string which passes over a frictionless pulley attached to the top of an inclined plane. The angle of inclination of the plane is θ. Take g=10ms−2
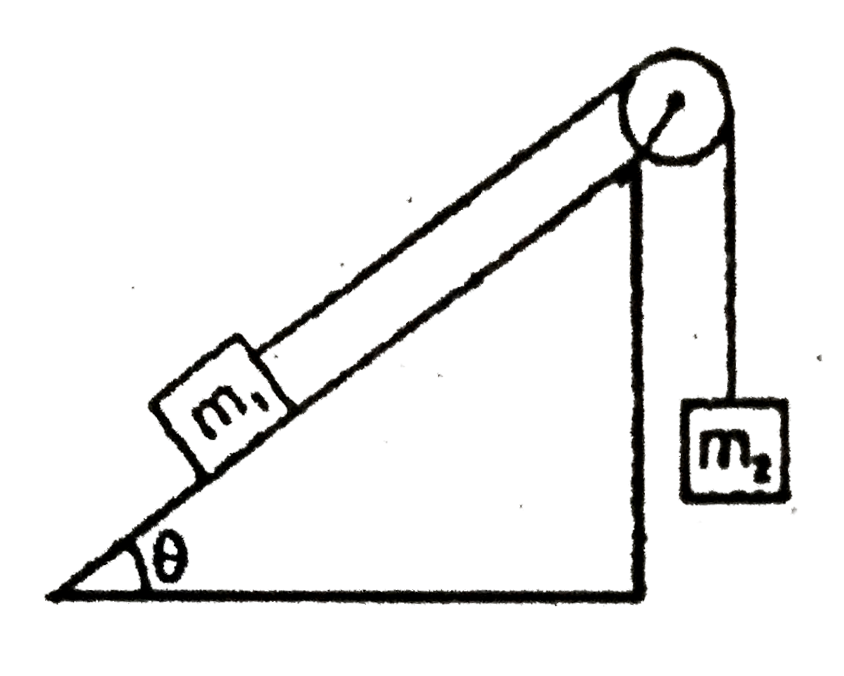
if m1=10kg,m2=5kg,θ=30∘, what is the acceleration of mass m2?
zero
(2/3)ms−2
5ms−2
10/3ms−2
The correct Answer is:A
a=(m2−m1sinα)g(m1+m2)=(5−10sin30∘)g(m1+m2)=0
Topper's Solved these Questions
Similar Questions
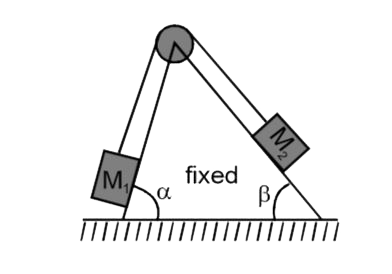
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
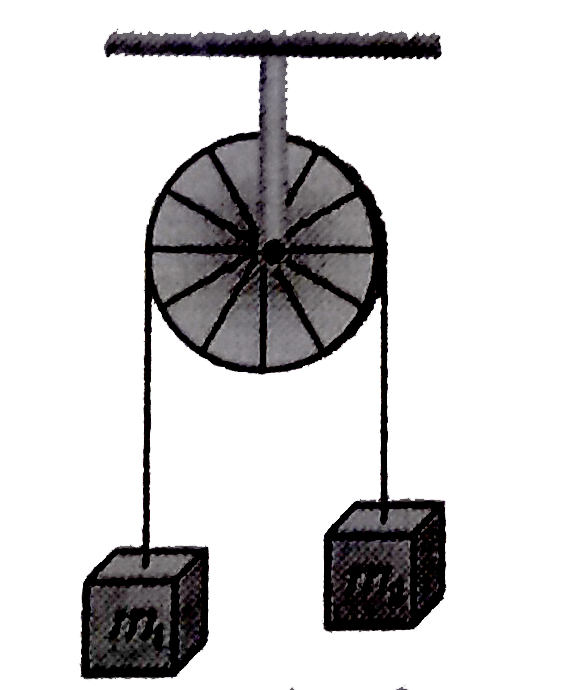
View SolutionTwo mass m1andm2 are attached to a flexible inextensible massless rope, which passes over a frictionless and massless pully. Find the accelerations of the masses and tension in the rope.

View Solution
Knowledge Check
Two masses M1andM2 are attached to the ends of string which passes over the pulley attached to the top of a double inclined plane. The angles of inclination of the inclined planes are αandβ. Take g=10ms−2. If M1=M2 and α=β, what is the acceleration of the system?
AzeroB2.5m/s−2C5m/s−2D10m/s−2Two masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?
 A10ms−2B5ms−2CzeroDnone of these
A10ms−2B5ms−2CzeroDnone of theseTwo masses m1 and m2 are connected to the ends of a massless string that passes over a pulley fixed at the top of a double incline as shown. Assuming m1>m2 acceleration of the system is:
 Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Am1gsinθ1+m2gsinθ2m1+m2Bm1gsinθ1−m2gsinθ2m1−m2Cm1gsinθ1−m2gsinθ2m1+m2D(m1+m2)(sinθ1+sinθ2)gm1−m2
Two masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo spheres of masses 3 kg and 4 kg are attached to ends of a string which passes over a frictionless pulley. Take g=9.8m/2. The relative acceleration of the system is
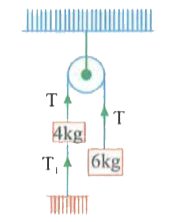
View SolutionTwo bodies of masses 4kg and 6kg are attached to the ends of a string which passes over a pulley, the 4kg mass is attached to the table top by another string.The tension in this string T1 is equal to
View SolutionTwo masses M1=5kg,M2=10kg are connected at the ends of an inextensible string passing over a frictionless pulley as shown. When masses are released, then acceleration of masses will be

View Solution
