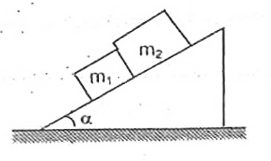
Two blocks m1=4kg and m2=2 kg connected by a weightless rod slide down a plane having an inclination of 37∘ . The coefficient of dynamic friction of m1 and m2 with the inclined plane are μ1=0.75 and μ2=0.25 respectively Find the common acceleration of the two blocks and tension in the rod Take is 37∘=0.6 and cos37∘=0.8 .
Let a be the common acceleration of the blocks and T be the tension in the connecting Components of wts of two blocks down the inclined plane
=m1gsin37∘+m2gsin37∘
=(m1+m2)gsin37∘
Frictional forces on two blocks up the inclined
plane =μ1m1gcos37∘+μ2m2gcos37∘
(μ1m1+μ2m2)gcos37∘
Net force down the plane =(m1+m2)a
∴(m1+m2)a=(m1+m2)gsin37∘
−(μ1m1+μ2m2)gcos37∘
Putting the valuse , we get a=1.3m/s2
To find T , we write eqn . of motion of block m1
T+m1gsin37∘−μ1m1gcos37∘=ma
on solving we get T=5.2N .

Similar Questions
Two blocks of masses m, = 4 kg and m, = 2 kg connected by a massless rod slide down on an inclined plane of inclination 37degree as shown in figure. If coefficient of friction of m1 and m2 with inclined plane are μ1=0.75andμ2=0.25 respectively, then tension (T) in the rod is (g=10ms−2)
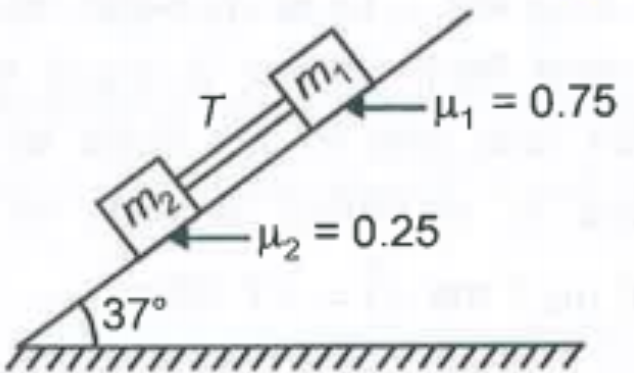
View SolutionIn the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
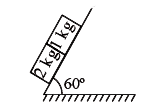
View Solution
Knowledge Check
Two blocks m1=4 kg and m2=2 kg connected by a weightless rod on a plane having inclination of 37∘ the coefficient of friction of m1 and m2 with the inclined plane are μ=0.25 each. Then the common accleration of the two blocks and the tension in the rod are
 A4m/s2,T=0B2m/s2,T=5NC4m/s2,T=10ND2m/s2,T=9N
A4m/s2,T=0B2m/s2,T=5NC4m/s2,T=10ND2m/s2,T=9NTwo equal masses m1=m2 = 1 kg are kept on an inclined plane with an initial separation of 0.4 m. The coefficients of friction μ1 and μ2 for the blocks m1 and m2 with ground are 0.1 and 0.2 respectively. If the collision between the two blocks is completely inelastic.
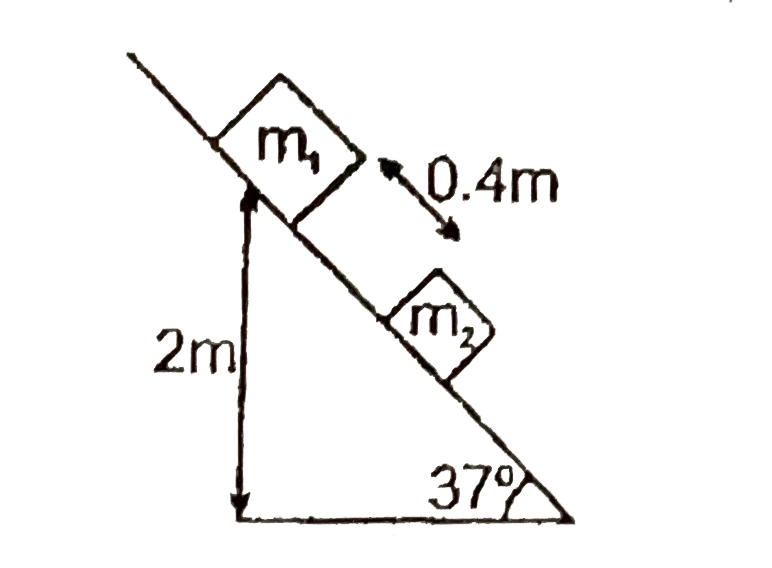 AThe loss in kinetic energy is 0.16 J.BThe loss in kinetic energy is 0.2 J.CThe speed of m1 just after collision is 4.8 m/s.DThe speed of m2 just after collision is 5 m/s.
AThe loss in kinetic energy is 0.16 J.BThe loss in kinetic energy is 0.2 J.CThe speed of m1 just after collision is 4.8 m/s.DThe speed of m2 just after collision is 5 m/s.A body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
AgsinαBμcosαCg(sinα−μcosα)Dg(cosα−μsinα)
Two blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.

View SolutionA rod of mass M and length L lies on an incline having inclination of θ=37∘. The coefficient of friction between the rod and the incline surface is μ=0.90. Find the tension at the mid point of the rod.
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
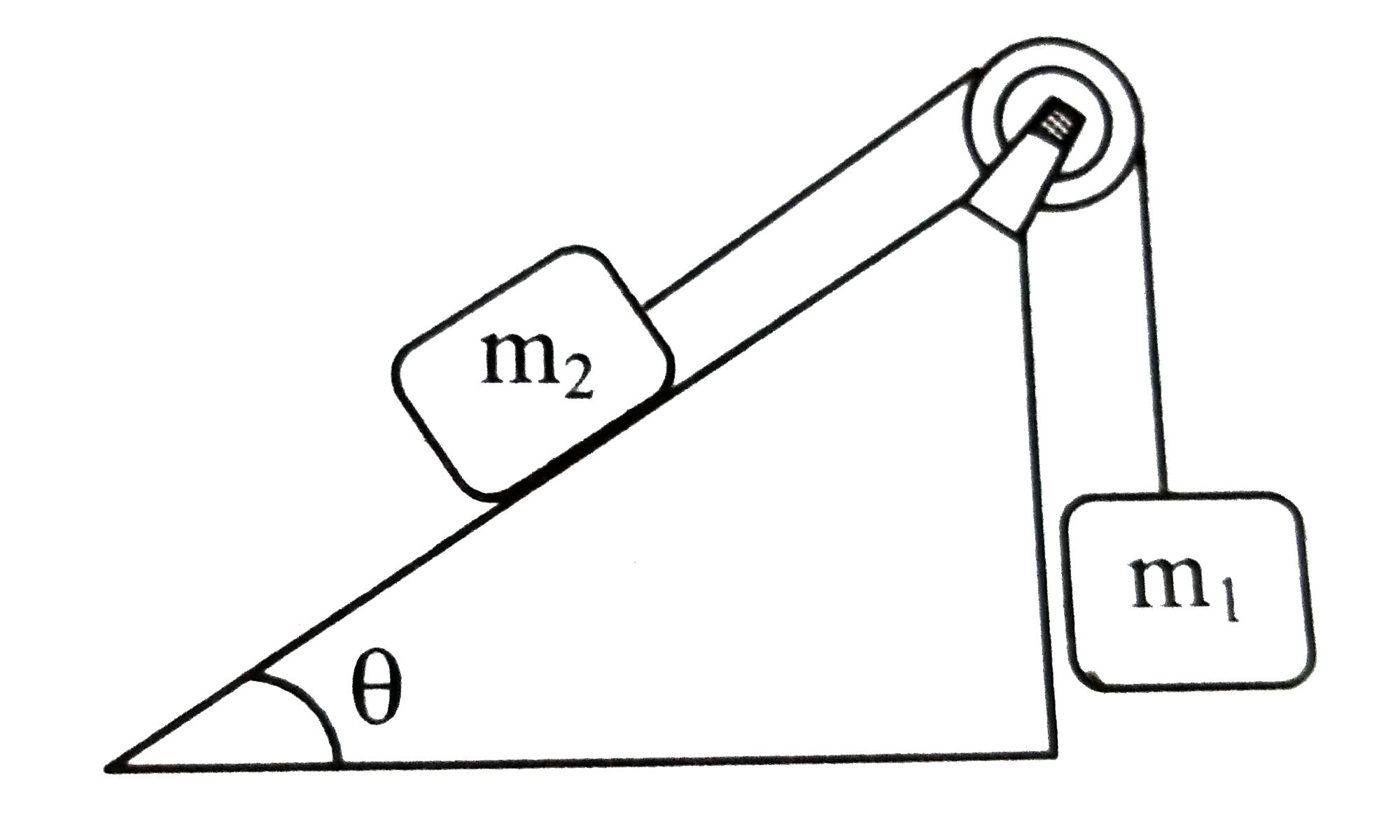
View SolutionTwo blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
View SolutionTwo blocks connected by a massless string slide down an inclined plane having angle of inclination 37º. The masses of the two blocks are M1 = 4 kg and M2 = 2 kg respectively and the coefficients of friction 0.75 and 0.25 respectively-

The common acceleration of the two masses is 1.3ms−2
b, The tension in the string is 14.7 N
c The common acceleration of the two masses is 2.94ms−2
d, The tension in the string is 5.29N
View Solution

