Two blocks of masses $m_{1} = 1 k g and m_{2} = 2 k g$ are connected by a string and side down a plane inclined at an angle $θ = 45^{\circ}$ with the horizontal. The coefficient of sliding friction between $m_{1}$ and plane is $μ_{1} = 0.4,$ and that between $m_{2}$ and plane is $μ_{2} = 0.2 .$ Calculate the common acceleration of the two blocks and the tension in the string.

Video Solution

Text Solution

Verified by Experts

As $μ_{2} < μ_{1},$ block $m_{2}$ has greater acceleration than $m_{1}$ if we separately consider motion of blocks. But they are connected so they move together as a system with common acceleration. So acceleration of the blocks :
$a = \frac{(m_{1} + m_{2}) g sin θ - μ_{1} g cos θ - μ_{2} m_{2} g cos θ}{m_{1} + m_{2}}$
$= \frac{(1 + 2) (10) (\frac{1}{\sqrt{2}}) - 0.4 \times 1 \times 10 \times \frac{1}{\sqrt{2}} - 0.2 \times 2 \times 10 \times \frac{1}{\sqrt{2}}}{1 + 2} = \frac{22}{3 \sqrt{2}} m s^{- 2}$
For block $m_{2} : m_{2} g sin θ - μ_{2} m_{2} g cos θ - T = m_{2} a \Rightarrow T = m_{2} g sin θ - μ_{2} m_{2} g cos θ - m_{2} a$
$= 2 \times 10 \times \frac{1}{\sqrt{2}} - 0.2 \times 2 \times 10 \times \frac{1}{\sqrt{2}} - 2 \times \frac{22}{3 \sqrt{2}} = \frac{2}{3 \sqrt{2}} N$

Updated on:21/07/2023

Two blocks of masses $m_{1}$ and $m_{2}$ are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between $m_{1}$ and plane is $μ$ .

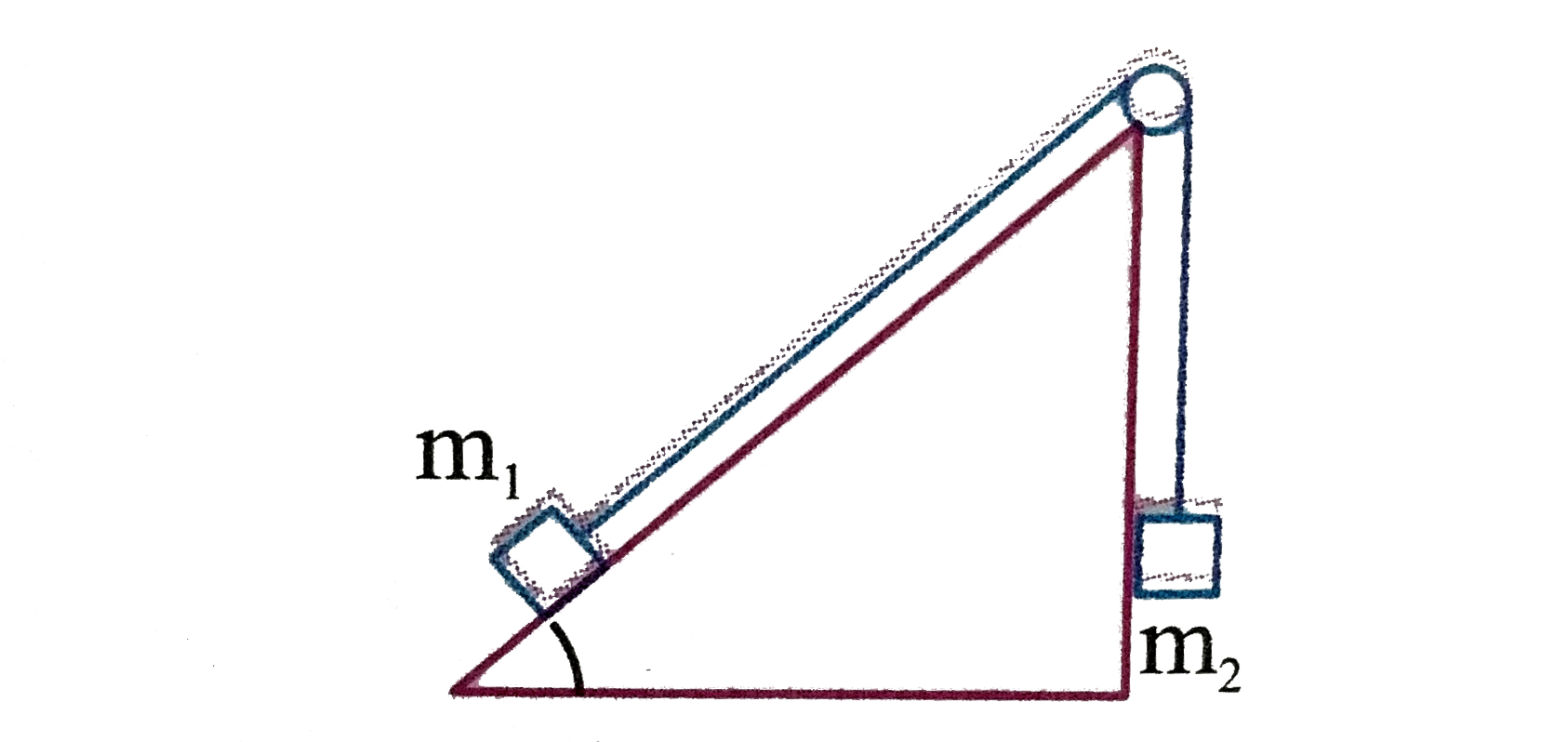AIf $m_{1} = m_{2}$ , the mass $m_{1}$ first begin to move up inclined plane when the angle of inclination $θ$ , then $μ = sec θ - tan θ$
BIf $m_{1} = m_{2}$ , then mass $m_{1}$ first begin to side down the plane if $μ = sec θ - tan θ$ .
CIf $m_{1} = 2 m_{2}$ , then mass $m_{1}$ first begins to slide down the plane if $μ = 2 tan θ$ .
DIf $m_{1} = 2 m_{2}$ , then mass $m_{1}$ first begins to slide down the plane if $μ = tan θ - \frac{1}{2} sec θ$ .
A block of mass m slides down an inclined plane which makes an angle $θ$ with the horizontal. The coefficient of friction between the block and the plane is $μ$ . The force exerted by the block on the plane is
A $m g cos θ$
B $\sqrt{μ^{2} + 1} m g cos θ$
C $\frac{μ m g cos θ}{\sqrt{μ^{2} + 1}}$
D $μ m g θ$
Two blocks are kept on an inclined plane and tied to each other with a mass-less string. Coefficient of friction between $m_{1}$ and inclined plane is $μ_{1}$ & that betweeb $m_{2}$ & the inclined is $μ_{2}$ . Then :

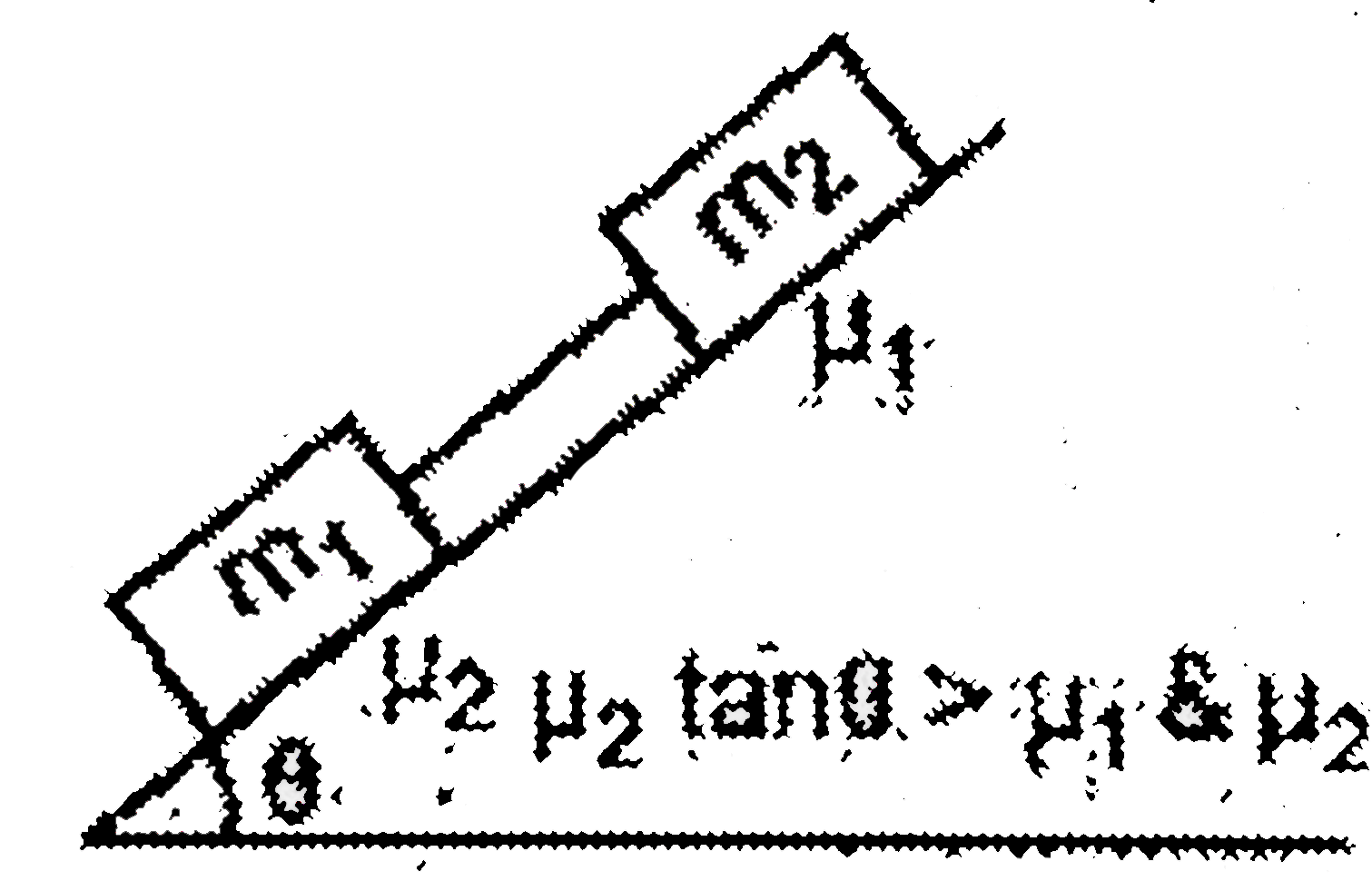AThe tension in the string in zero if $μ_{1} > μ_{2}$
BThe tension in the string is zero if $μ_{1} < μ_{2}$
CTension in the string is always zero irrespective of $μ_{1} & μ_{2}$
DNone of these