In Fig. what should be the speed of the charged particle so that it cannot collide with the upper wall? Also, find the coordinates of the point where the particle strikes the lower plate in the limiting case of velocity.
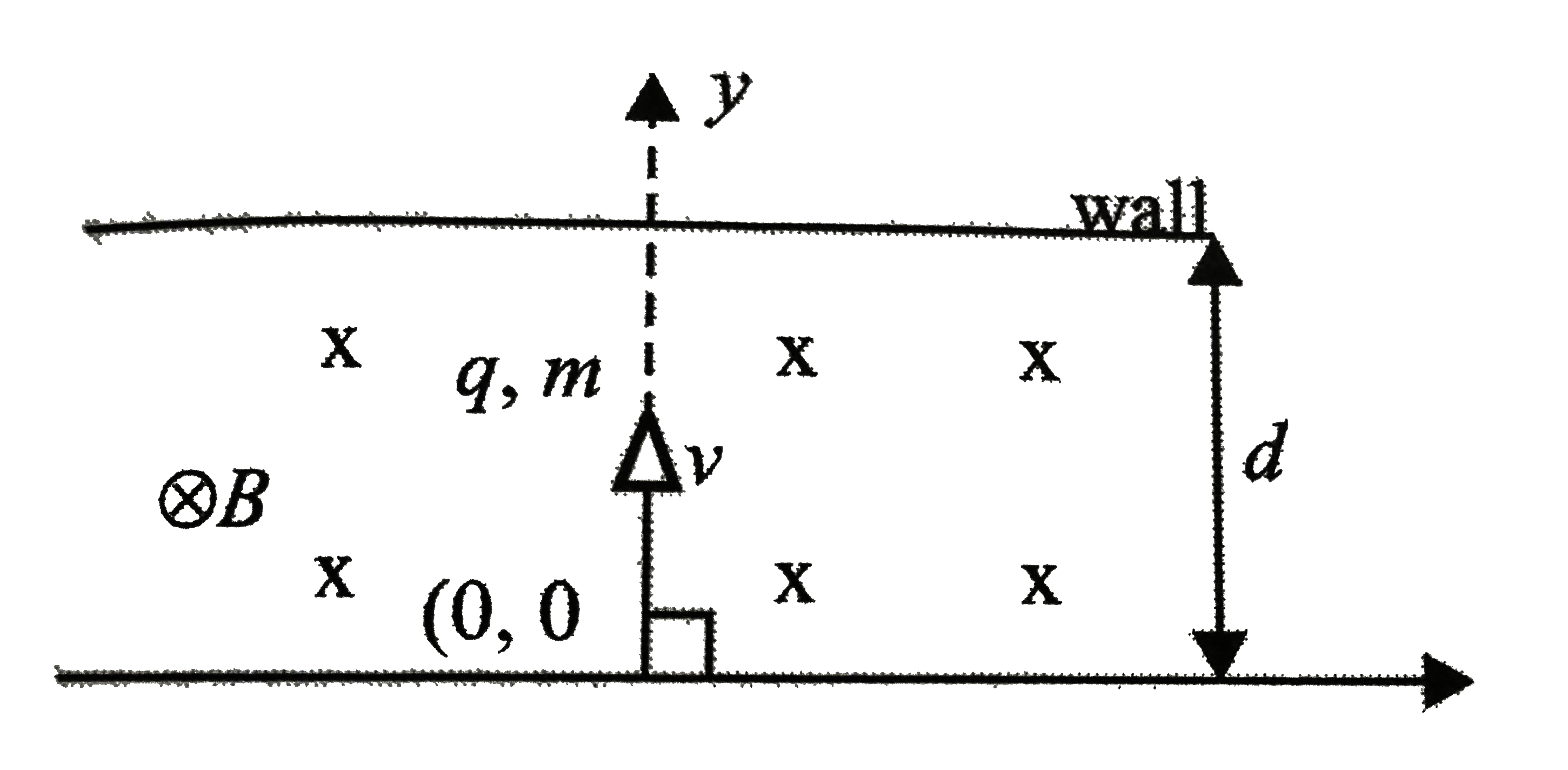
(i) The path of the particle will be circular larger the velocity , larger will be the radius. For particle not to a strike R<d
∴mvqB<d⇒<qBdm.

(ii) for limiting case v=qBdm
R=d
∴ coordinate =(−2d,0,0)l

Topper's Solved these Questions
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - QUESTIONS FOR PRACTICE
34 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 1 SECTION -A :- Magnetif field due to straight wire
10 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-II)
40 Videos
- MATTER WAVEBOOK - MOTIONCHAPTER - MATTER WAVEEXERCISE - EXERCISE 3 (SECTION B)
7 Videos
Similar Questions
A particle of mass m and charge q is accelerated by a potential difference V volt and made to enter a magnetic field region at an angle θ with the field. At the same moment, another particle of same mass and charge is projected in the direction of the field from the same point. Magnetic field induction is B. What would be the speed of second particle so that both particles meet again and again after regular interval of time. Also, find the time interval after which they meet and the distance travelled by the second particle during that interval.
View SolutionA particles is projected horizontally with a speed v from the top of a plane inclined at an angle tehta to the horizontal as shown in the figure.
(a) Hwo far from the point of projection will the particle strike the plane ?
(b) Find the time taken by the particel to hit the plane.
(c) What is the velocity of particle just before it hits the plane ?
View Solution
Knowledge Check
A particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.A2u2(1+cos2θ)3/2g2√2cosθBu2(1+cos2θ)3/2g2√2cosθCu2(1−sin2θ)3/2g2√2cosθDu2(1−tan2θ)3/2g2√2cosθA charged particle is projected with a certain velocity between the plates with opposites charges. The magnetic field is also applied between the plates so that the particle moves undeflected and hits the plate A. The force experienced by the plate is F1. Now if the particle is projected with double of the initial velocity with smaller conditions, the force experienced by the plate is F1/F2 is :
 A2B12C14D1.0
A2B12C14D1.0
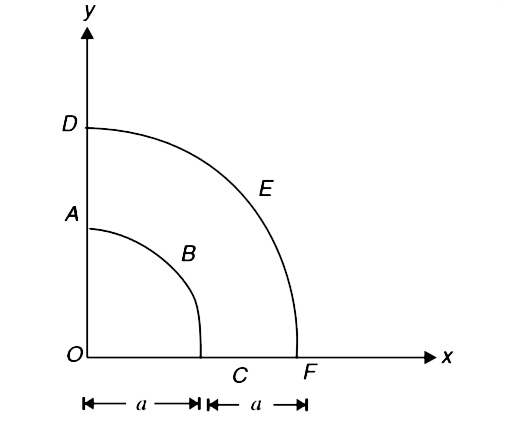
ABCFED is a uniform plate (shown in figure). ABC and DEF are circular arcs with common centre at O and having radii a and 2a respectively. This plate is lying on a smooth horizontal table. A particle of mass half the mass of the plate strikes the plate at point A while travelling horizontally along the x direction with velocity u. The particle hits the plate and rebounds along negative x with velocity u2 . Find the velocity of point D of the plate immediately after the impact. [Take 289π≅1 ]
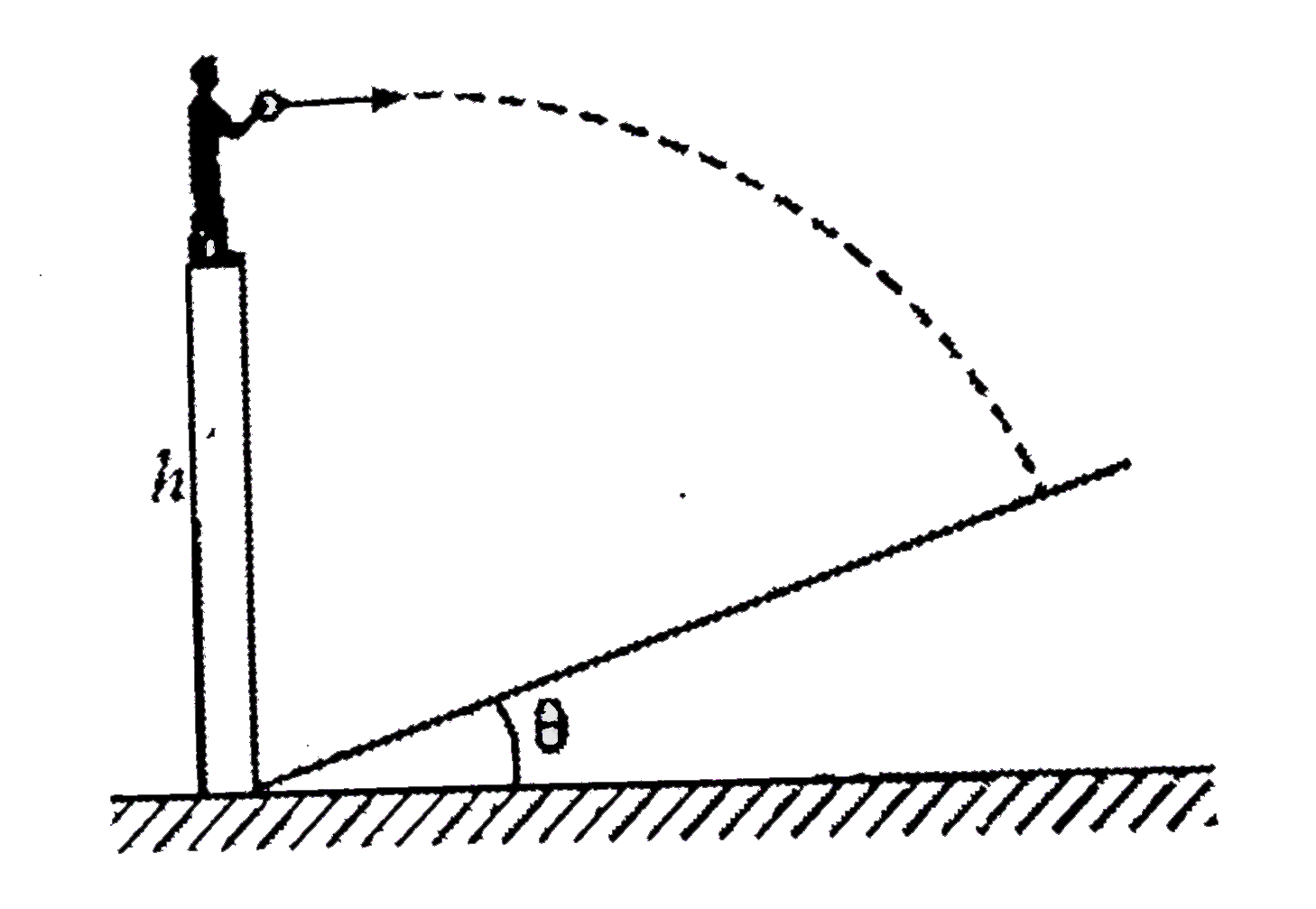
View SolutionA partacle is thrown in horizontal direction with speed u from a point P, the top of a tower shown in figure.1.49 at a vertical height h above the inclined plane of inclination θ. Find the speed with which the particle is thrown so that it strikes the plane normally. Also find the distance from the foot of the tower where the particle will strike.
View SolutionIn the figures shown, three particles are thrown from a tower of height 40 m as shown in figure. In each case find the time when the particles strike the ground and the distance of this point from foot of the tower.
 ,
,  ,
,  .
.
View Solution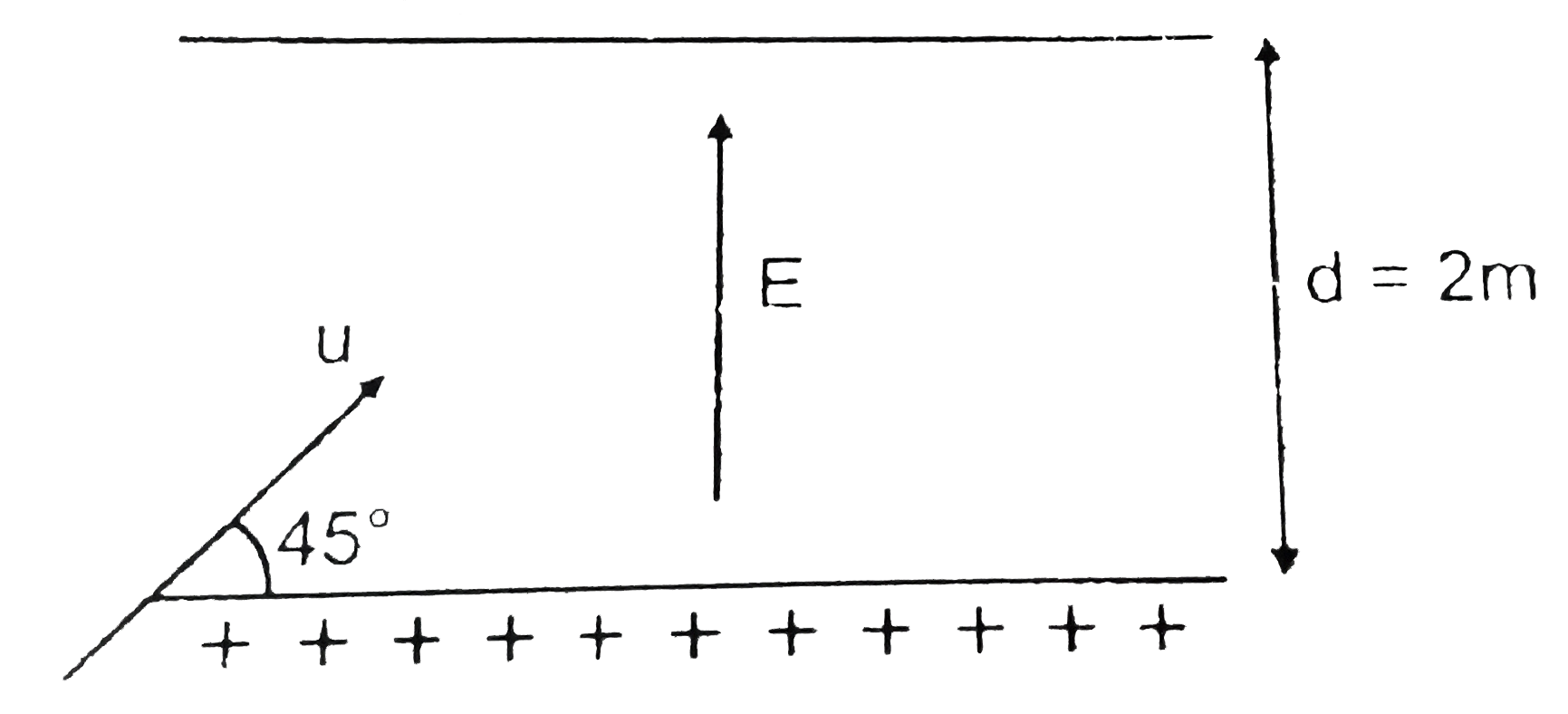
An electron is projected as shown with speed u. If electron just fails to strike the upper plate, find range. (distance from starting point at which electron strike the lower plate again). Consider only electric force.
View SolutionEarth and moon centre distance is 'r'. From the mid point what should be the speed of the particle so that it can escape to infinity?
View SolutionA particle with specific charge q/m moves in the region of space where there are unifrom mutually perpendicular electric and magnetic fields with strength E and induction B (fig). At the moment t=0 the particle was located at the point O and had zero velocity. For the non-relativistic case find:
(a) the law of motion x(f) and y(t) of the particle, the shape of the trajectory,
(b) the lenght of the segment of the trajectory between two nearest points at which the velocity of the particle turns into zero,
(c) the mean value of the particle's velocity vector projections on the x axis (the drift velocity).
View Solution
