As shown in figure AB represents an infinite wall tangential to a horizontal semi circular track.O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively 'V' and 'a' then,
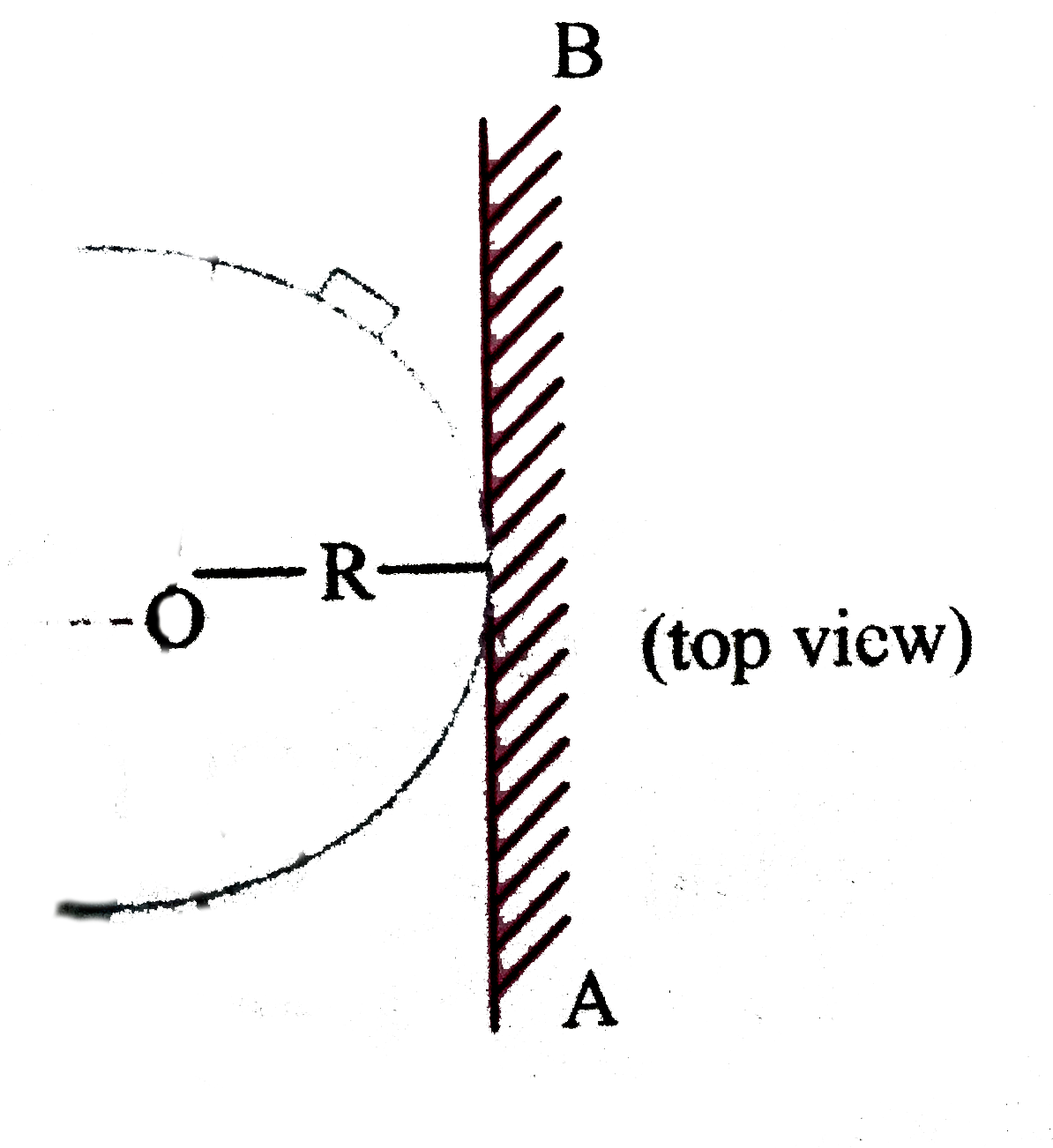
V=vcos(vt)R
V=vsec2(vtR)
a=v2Rsec2(vtR)tan(vtR)
a=2v2Rsec2(vtR)tan(vtR)
The correct Answer is:B, D

tanθ=yR,y=Rtanθ
v=dydt=Rsec2θ(dθdt)=Rω2sec2θ
=vsec2(vtR)
Acceleration of the shadow :
a=dvdt=2v2Rsec2(vtR)tan(vtR)
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason
12 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Matrix - Match
5 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A man running along a circular track has the speedof 10 km per hour. A source of light is at the centre of the circular track. A wall is along the tangent to the circular track at the point from which he starts.What is the speed of the shadow of the man on the wall when he covers 18th of the track? (Assume thetrack to be a line.)
View SolutionA point moves along a circle with a velocity v=t/2. Find the acceleration of the point at the moment when it has covered a quarter circle from the beginning of motion.
View Solution
Knowledge Check
As shown below AB represents an infinite wall tangential to a horizontal semi-circular track. O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively V and a, then :
 AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR)
AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR)On a particle moving on a circular path with constant speed v, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
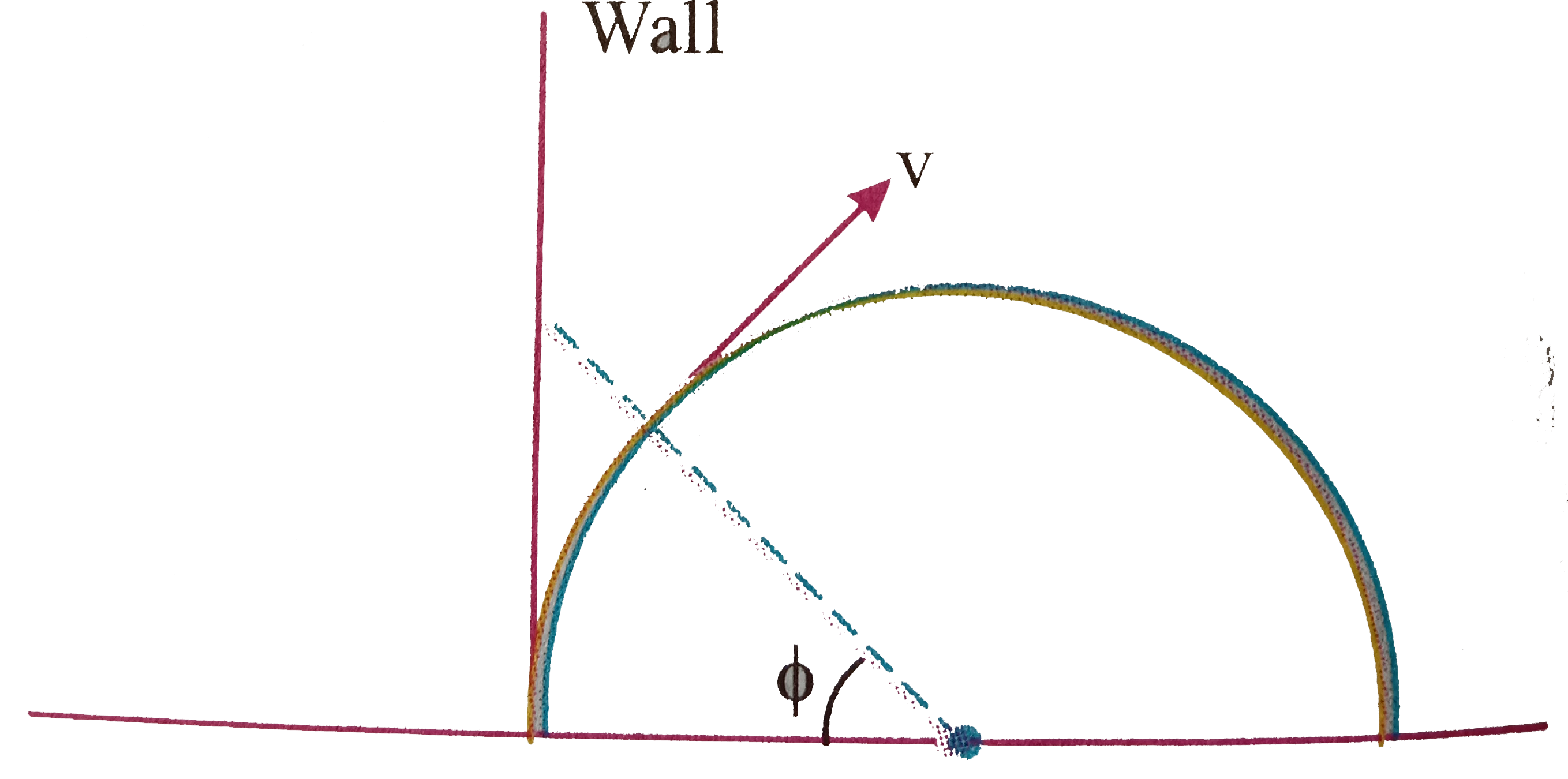 Avsec2φBvcos2φCvcosφDNone of these
Avsec2φBvcos2φCvcosφDNone of theseA block of mass m is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
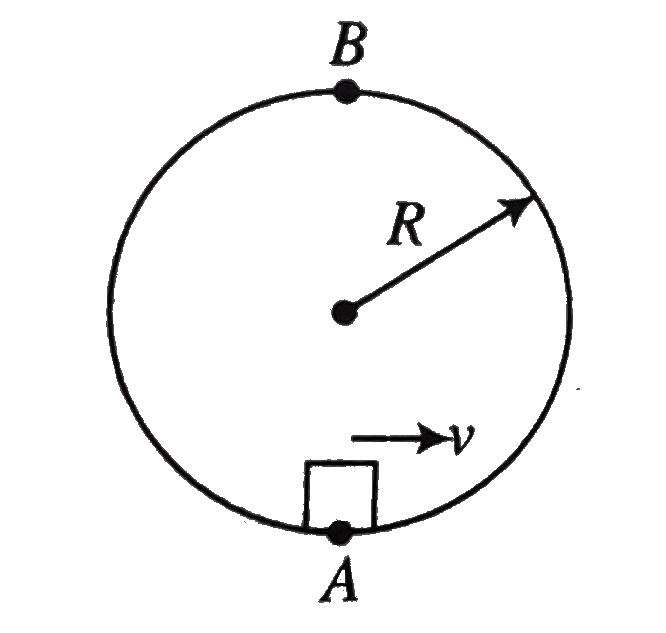 Amv2RBmv2πRC2mv2RD2mv2πR
Amv2RBmv2πRC2mv2RD2mv2πR
A rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
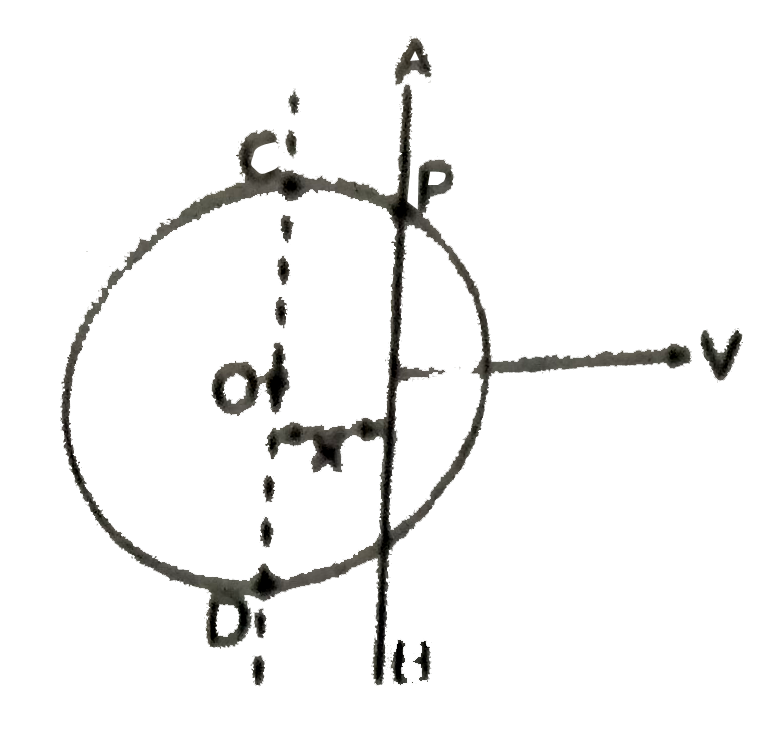
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View SolutionA point moves along an arc of a circle of radius R. Its velocity depends on the distance covered s as v=√s, where a is a constant. Find the angle α between the vector of the total acceleration and the vector of velocity as a function of s.
View SolutionA point moves along a circle with velocity v = at where a 0.5 m/sec2. Then the total acceleration of the point at the moment when it covered (1/10) th of the circle after beginning of motion -
View SolutionA truck has to move to a dimetrically opposite point on a circular track which surrounds a field. The speed of the truck along the track is 2v0. While that in the field is v0. The driver plans to move along an arc of a circle and then along a straight line as shown.
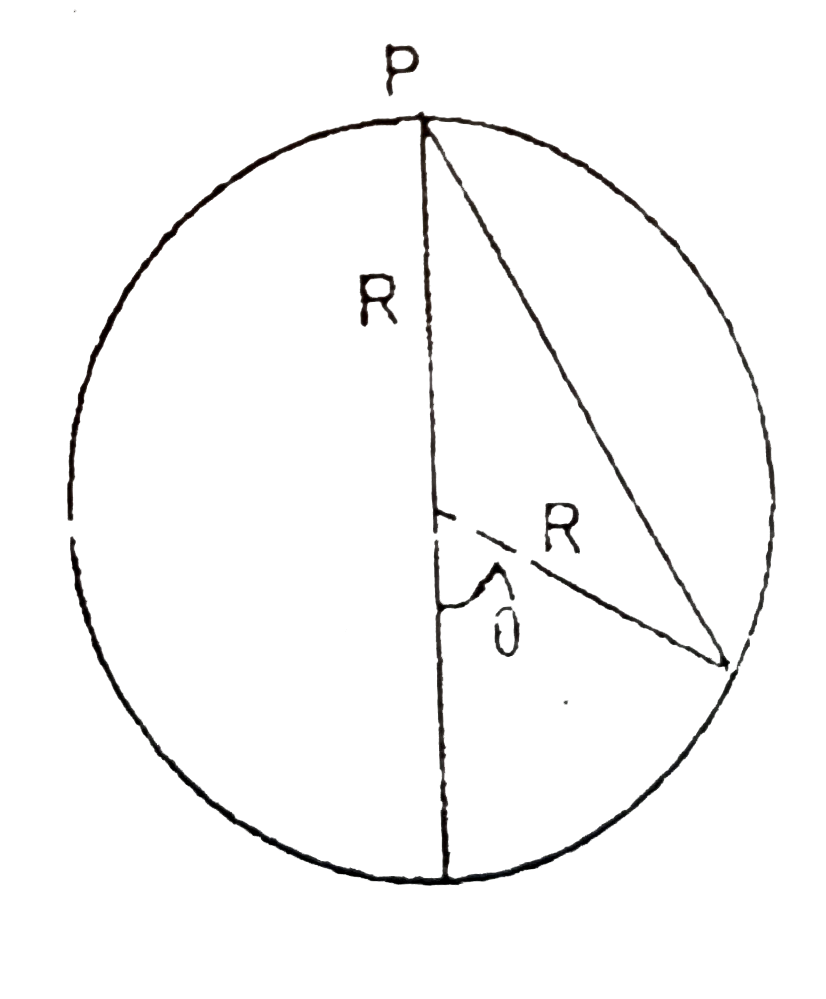
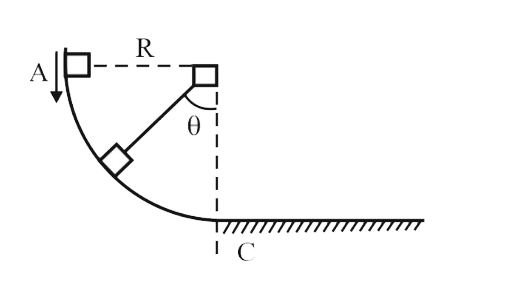
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
View Solution
