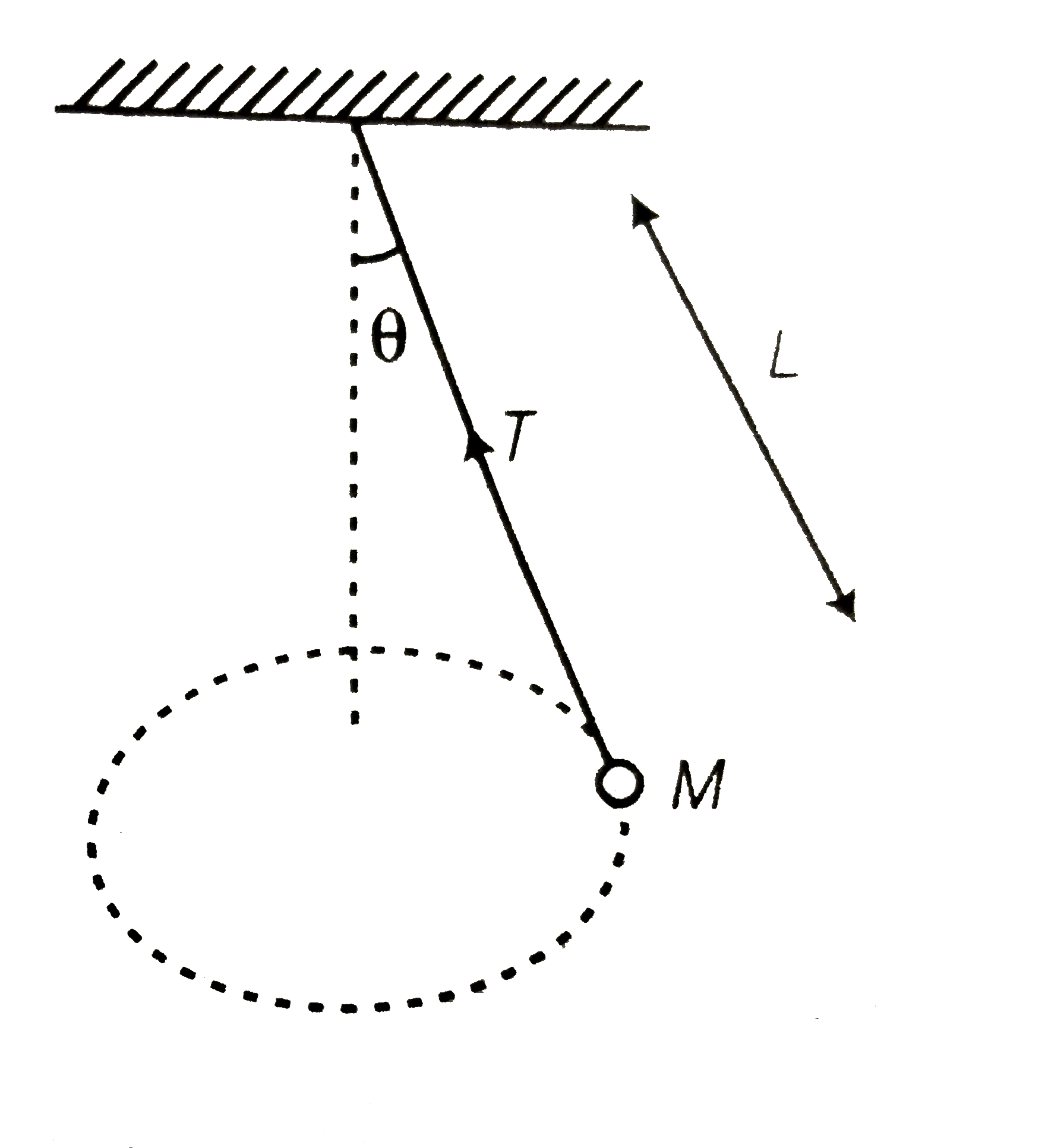
A string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes $2 / π$ revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.

Video Solution

Text Solution

Verified by Experts

As shown in Fig. 7.67, for vertical equilibrium of mass m
$T cos θ = mg \dots \dots (i)$
While for circular motion
$T sin θ = (m v^{2} / r) = m r ω^{2} \dots \dots . . (i i)$
(a) So , from Eqn . (ii) , $T = [m r ω^{2} / sin θ] = m L ω^{2}$
[as r = L sin $θ$ ]
$∴ T = 10^{- 1} \times 1 \times 4^{2} = 1.6 N$ [ as $ω = 2 π f = 2 π \times (2 / π) = 4]$
(b) From Eqn. (i) , cos $θ = \frac{mg}{T} = \frac{10^{- 1} \times 10}{1.6} = \frac{5}{8}$ ,
i.e., $θ = {cos}^{- 1} (5 / 8)$
(c) $v = r ω = L sin θ \times ω$ [ as r = L sin $θ$ ]
or $v = 1 \times 0.78 \times 4 = 3.12$ m/s [ as sin $θ = 0.78$ ]

Updated on:21/07/2023

A string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes (2/ $π$ ) revolutions per second around vertical axis through the fixed end. Calculate the tension in the string-
A1.0 N
B1.6 N
C2N
D4N
A string of length $l = 1 m$ is fixed at one end carries a mass of 100gm at other end. The string makes $\sqrt{5} / (π)$ revolutions per second about a verticle axis passing through its second end. What is the angle of inclination of the string with the vertical?
A $30^{\circ}$
B $45^{\circ}$
C $60^{\circ}$
D $75^{\circ}$
A string of length $L$ is fixed at one end and carries a mass $M$ at the other end. The string makes $2 / π$ revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.

AML
B2ML
C4ML
D16ML