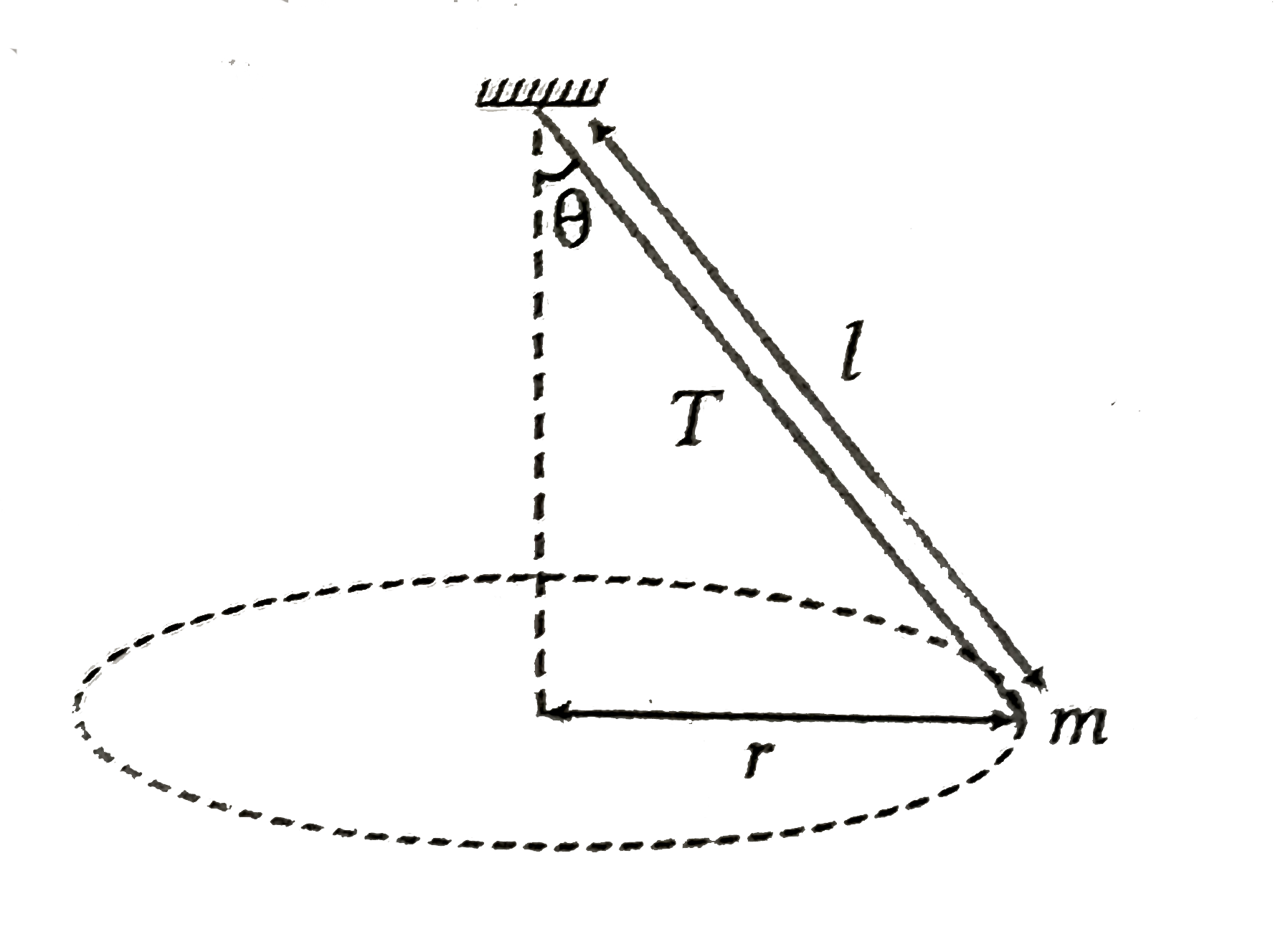
A string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
16 ml
4 ml
8 ml
2 ml
The correct Answer is:A
Balancing horizontal forces,
Tsinθ=mrω2
or Tsinθ=m(lsinθ)ω2
∴ T=mlω2=ml(2πf)2
=ml(2π×2π)2=16ml
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
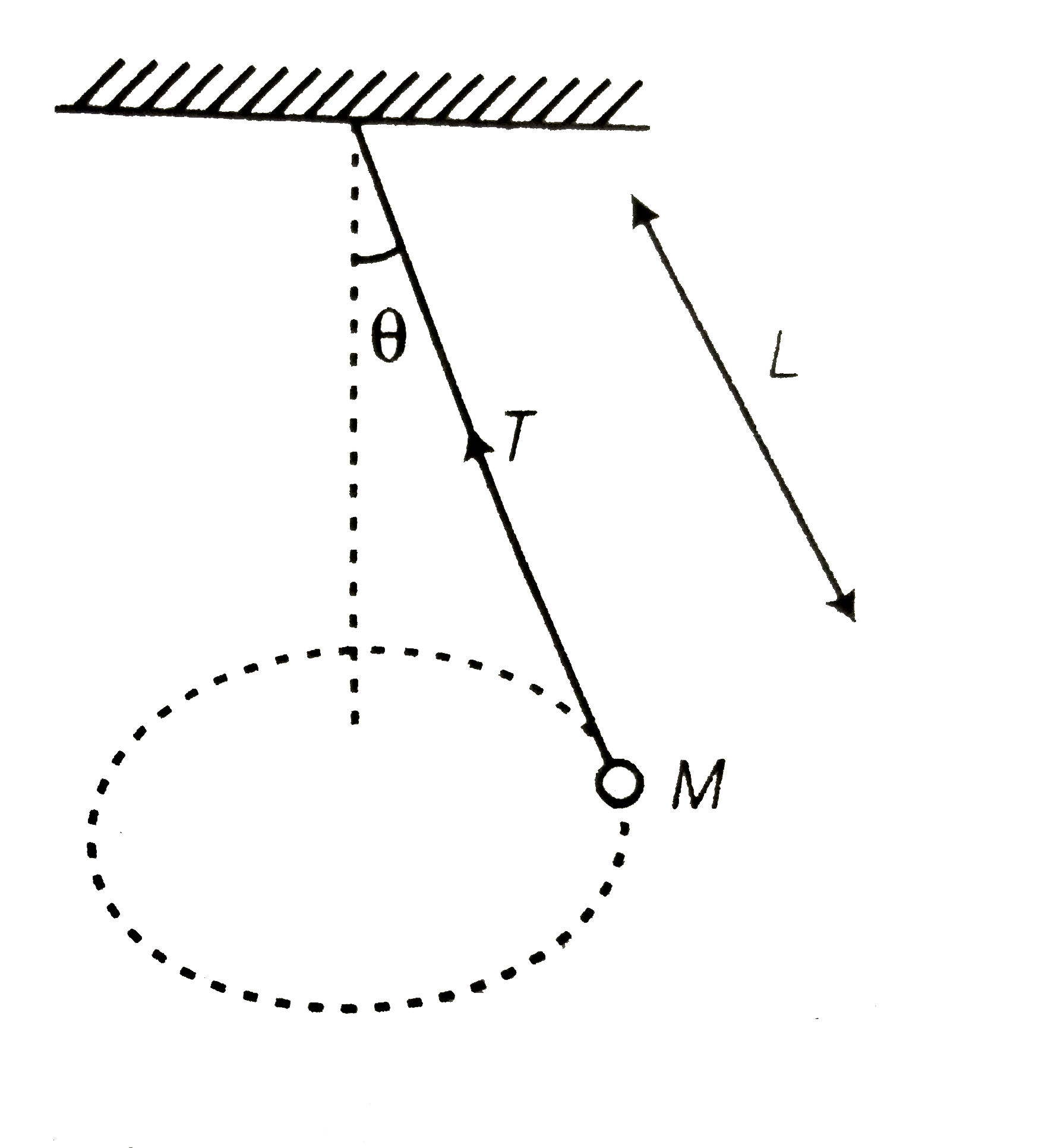
A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
View SolutionA string of length 50cm is fixed at one end and carries a mass of 200g at the other end. The string makes 5/2π revolution per second around the verticle axis through the fixed end. Calculate (a) the tension in the string (b) the angle of incilination of the string with verticle and (c) linear velocity of the mass.
View Solution
Knowledge Check
A string of length l fixed at one end carries a mass m at the other end. The strings makes 2πrevs−1 around the axis through the fixed end as shown in the figure, the tension in the string is
 A16 mlB4 mlC8 mlD2 ml
A16 mlB4 mlC8 mlD2 mlA string of length L is fixed at one end and carries a mass M at the other end. The string makes 2/π revolution per second around the vertical axis through the fixed end as shown in the figure, then tension in the string is.
 AMLB2MLC4MLD16ML
AMLB2MLC4MLD16MLA string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes (2/π) revolutions per second around vertical axis through the fixed end. Calculate the tension in the string-
A1.0 NB1.6 NC2ND4N
A string of length 1 m is fixed at one end and carries a mass of 100 gm at the other end. The string makes 2/πrevolutions per second about a vertical axis through the fixed end. The angle of inclination of the string with the vertical, and the linear velocity of the mass will respec- tively be - (in M.K.S. system)
View SolutionVibrations of string fixed at one end
View SolutionA string of length 1m is fixed at one end and carries a mass of 1 kg at the other end. The string makes 2/π revolutions per second around a vertical axis passing through the fixed end. Calculate (i) angle of inclination of the string with the vertical, (ii) the tension in the strong and (iii) the linear velocity of the mass.
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100g and the string makes 4radpersec around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View SolutionIn a conical pendulum arrangement, a string of length 1 m is fixed at one end with a bob of mass 100 g and the string makes 2πmvs−1around a vertical axis through a fixed point. The angle of inclination of the string with vertical is: (Take g=10ms−1)
View Solution

