A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
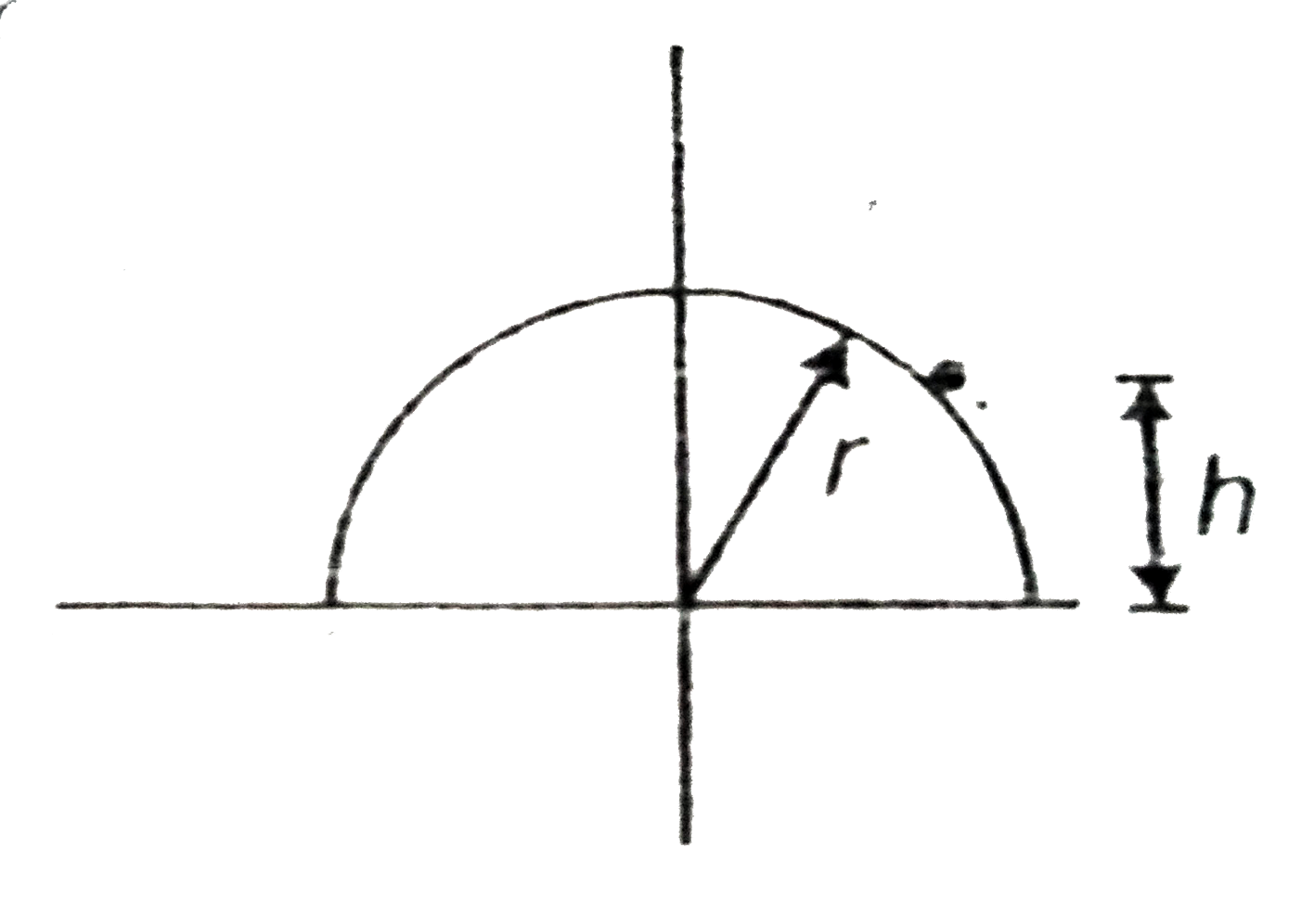
h=r2
h=r3
h=2r3
h=r4
The correct Answer is:C
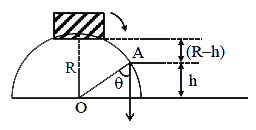
When released from top with zero velocity block leaves contact at
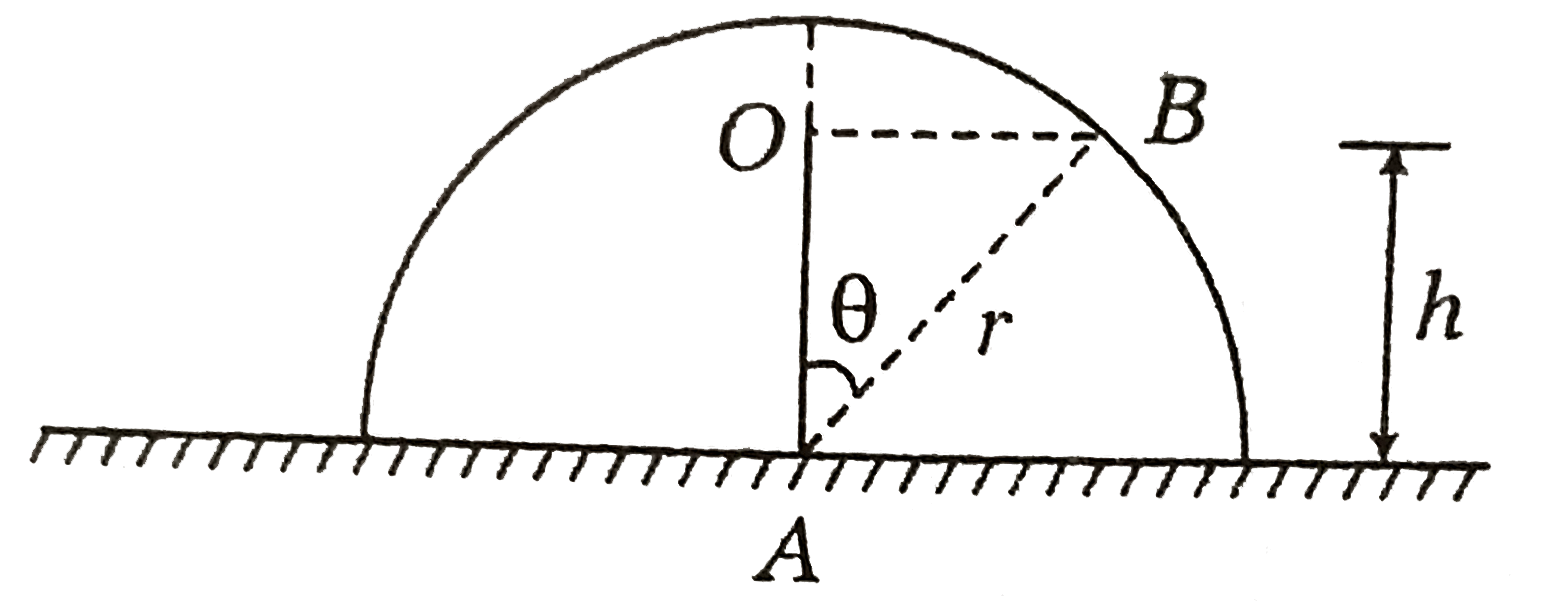
cosθ=23
∵InΔAOB,
cosθ=OAAB⇒cosθ=hr
∴ h=rcosθ=2r3
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A small body of mass m slides without friction from the top of a hemisphere of radius r. At what hight will the body be detached from the centre of hemisphere?
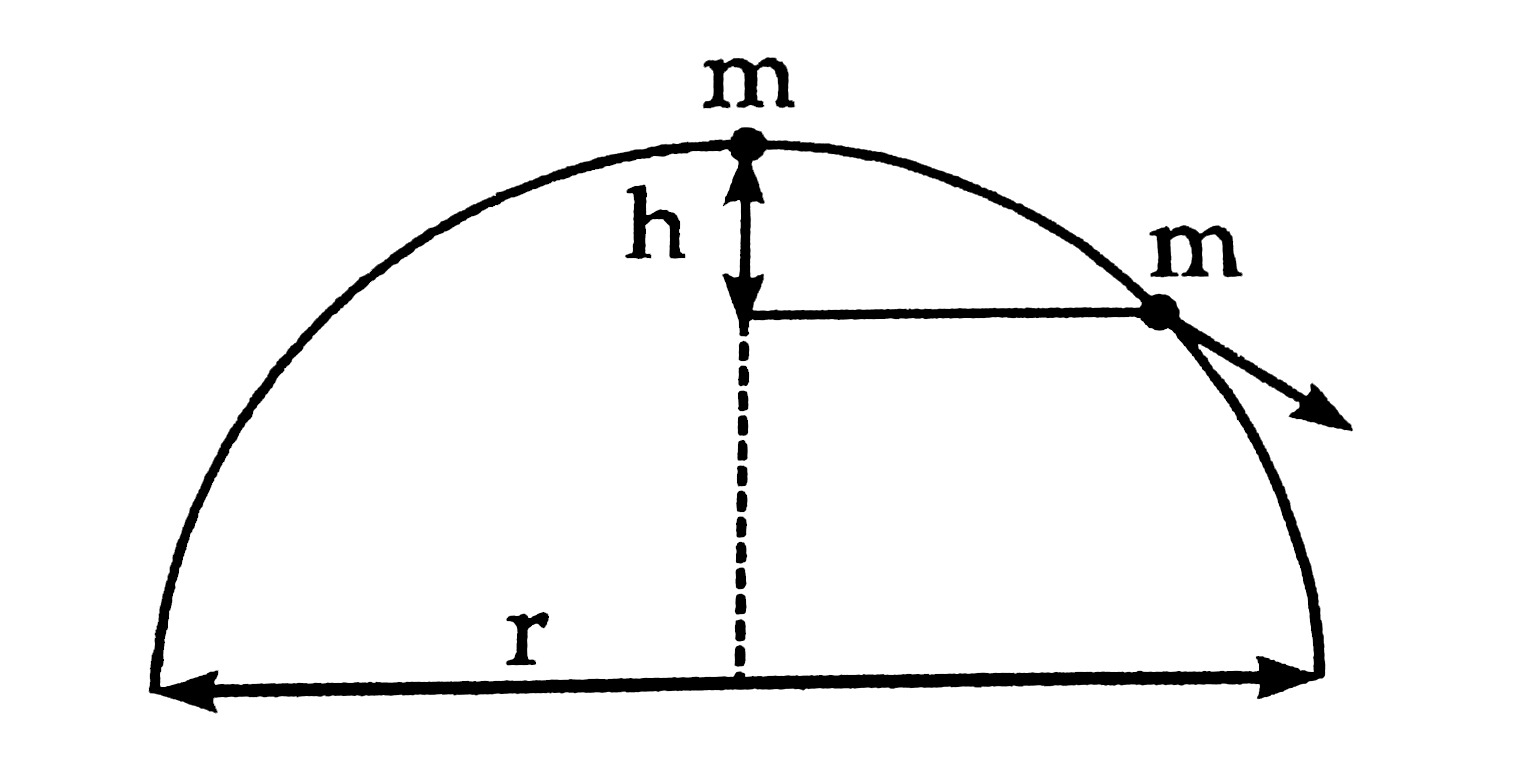
View SolutionA small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View Solution
Knowledge Check
A small body of mass m can slide without friction along a through bent which is in the form of a semi-circular arc of radius R. At what height h will the body be at rest with respect to the trough, if the trough rotates with uniform angular velocity ω about a vertical axis:
 ARBR−2gω2CR+2gω2DR−gω2
ARBR−2gω2CR+2gω2DR−gω2A small body of mass m slides without friction from the top of a hemisphere of radius r. At what height will the body be detached from the surface of hemisphere?
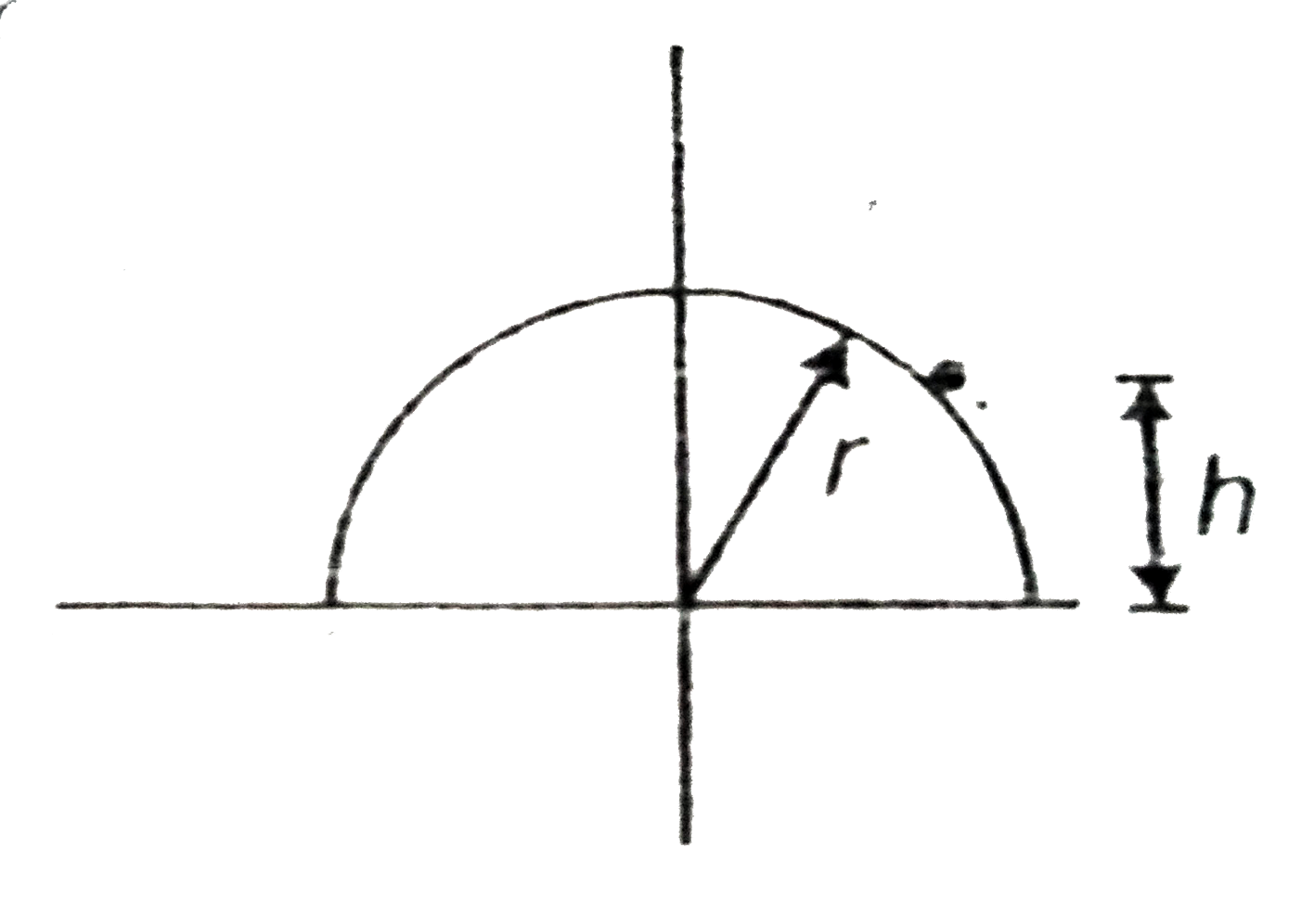 A32rB23rC12gt2Dv22g
A32rB23rC12gt2Dv22gThe total surface area of a solid hemisphere of radius r is
Aπr2B2πr2C3πr2D4πr2
Determine the position of the centre of mass of a hemisphere of radius R.
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
View SolutionA small block slides down from the top of hemisphere of radius R = 3 m as shown in the figure. The height 'h' at which the block will lose contact with the surface of the sphere is __________ m.
(Assume there is no friction between the block and the hemisphere)
View SolutionA small disc is on the top of a hemisphere of radius R. What is the smallest horizontal velocity v that should fbe given to the disc for it to leave the hemisphere and not slide down it?[There is no friction]
View SolutionA body of mass Mkg is on the top point of a smooth hemisphere of radius 5m . It is released to slide down the surface of hemisphere it leaves the surface when its velocity is 5ms−1 At this instant the angle made by the radius vector of the body with the vertical is ( Take g=10m/s2)
View Solution

