A body is moving down a long inclined plane of angle of inclination 'θ' for which the coefficient of friction varies with distance x as μ(x) = kx , where k is a constant . Here x is the distance moved by the body down the plane . The net force on the body will be zero at a distance x0 is given by ..........

F = mg sin θ−f
N = mg cos θ , f=μN=μmgcosθ
F=mg sinθ=μmg cosθ
F=mg(sinθ−kxcosθ)
If F = 0 , sinθ−kx0cosθ=0⇒x0=tanθk
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice
23 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - OBJECTIVE QUESTIONS ( only one choice is correct )
80 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension
12 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston
14 Videos
Similar Questions
A body is moving down along inclined plane of angle of inclination theta The coefficient of friction between the body and the plane varies as mu=0.5x where x is the distance moved down the plane. The body will have the maximum velocity when
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View Solution
Knowledge Check
A body which was released from rest, slides down on an inclined plane of inclination θ. The coefficient of friction dowh the plane varies as μ=kx where k is a spositive constant and x is the distance moved by the body down the plane. The speed of the body 'v' versus distance 'x' graph will be as :
A B
B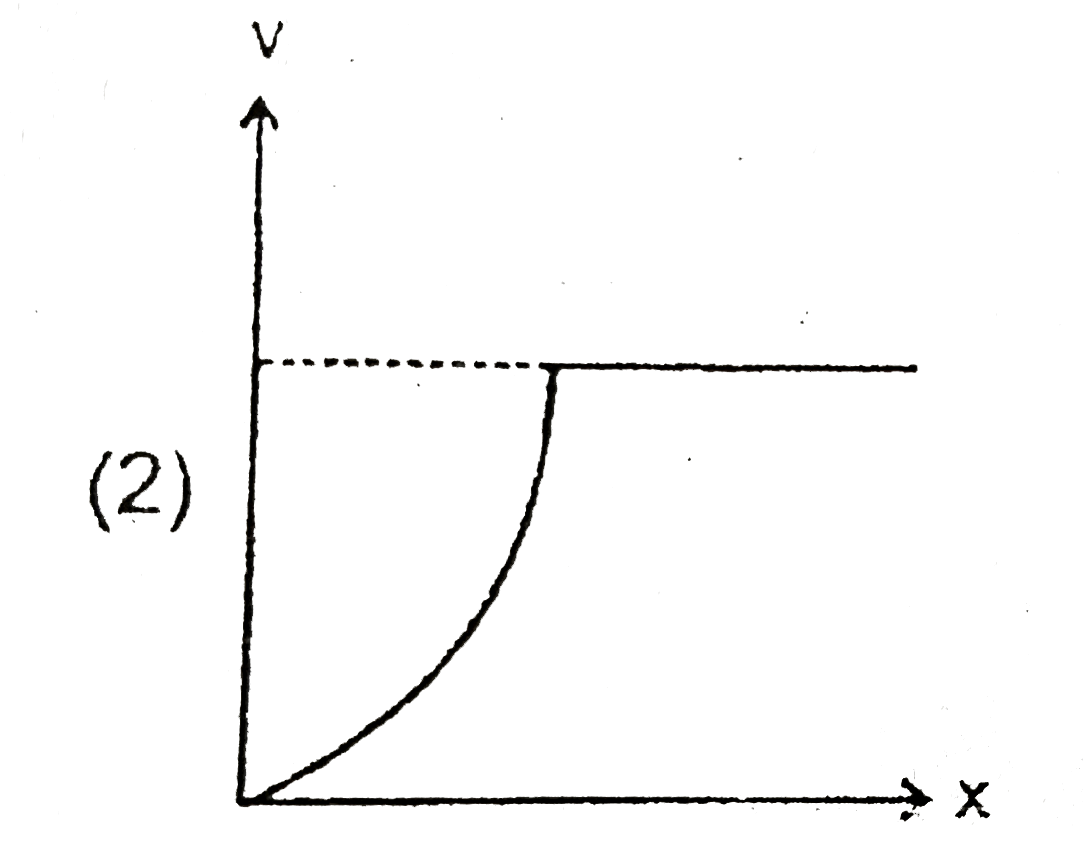 C
C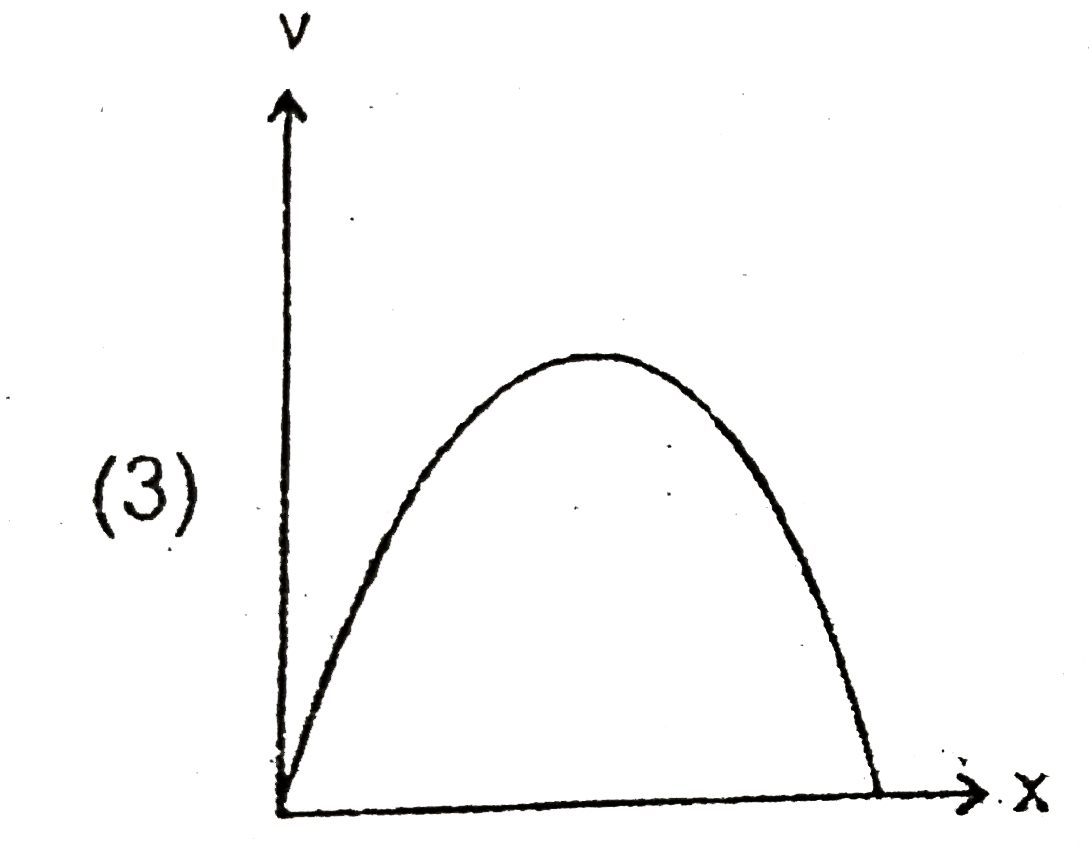 D
D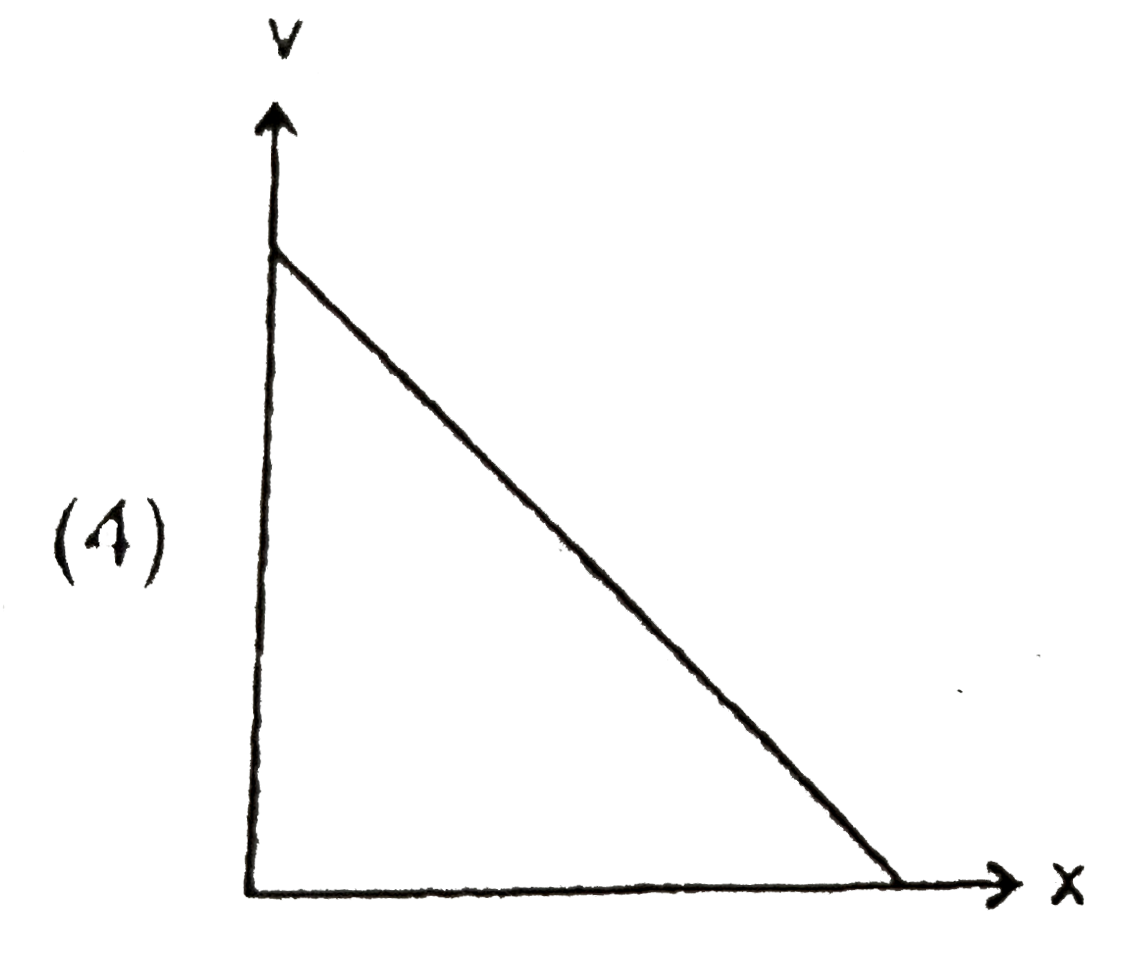
A body is moving down a long inclined plane of angle of inclination θ. The coefficient of friction between the body and the plane varies as μ−0.1x, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by :
Ax=10tanθBx=5tanθC√2cotθDx=√10cotθA body is moving down a long inclined plane of inclination 45∘ with horizontal. The coefficient of friciton between the body and the plane varies as μ=x/2, where x is the distance moved down the plane. Initially x=0&v=0
AWhen x=2 the velocity of the body is √g√2m/sBThe velocity of the body increases all the timeCAt an instant when v≠0 the instantaneous acceleration of the body down the plane is g(2−x)2√2DThe body first accelerates and then, decelerates.
A body is moving down a long inclined plane in inclination 45∘ with horizontal. The coefficient of friction between the body and the plane varies as μ=x/2, where x is the distance moved down the plane. Initially
x=0&v=0.
View SolutionA small mass slides down an inclined plane of inclination θ the horizontal the coefficient of friction is m=μ0x, where x is the distance by the mass before it stops is .
View SolutionWhen a body of mass M slides down an inclined plane of inclination θ, having coefficient of friction μ through a distance s, the work done against friction is :
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizontal. If the coefficient of friction is 0.3 then acceleration of the body is
View SolutionA body is sliding down an inclined plane forming an angle 30∘ with the horizantal. If the coefficient of friction is0.3 then acceleration of the body is
View Solution