Question

A body is sliding down an inclined plane forming an angle ${30}^{\circ }$ with the horizantal. If the coefficient of friction is$0.3$ then acceleration of the body is

Options

A. `1.25.ms^(-2)`
B. `2.35 ms^(-2)`
C. `3.4ms^(-2)`
D. `4.9ms^(-2)`

Answer

B

Explanation

To find the acceleration of a body sliding down an inclined plane at an angle of $${30}^{\circ }$$ with a coefficient of friction of $$0.3$$, we can follow these steps:

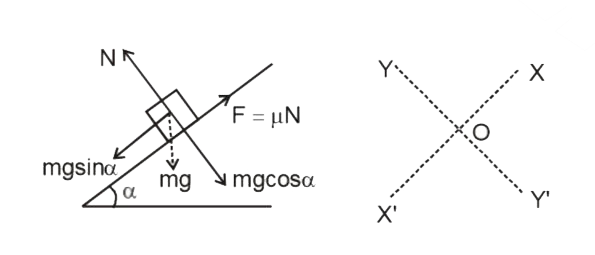
Step 1: Identify the forces acting on the body
The forces acting on the body are:
1. Gravitational force (\(Mg\)) acting downwards.
2. Normal force (\(N\)) acting perpendicular to the inclined plane.
3. Frictional force (\(f\)) acting opposite to the direction of motion.

Step 2: Resolve the gravitational force into components
The gravitational force can be resolved into two components:
- Parallel to the incline: \(F_{\text{parallel}} = Mg \sin \theta\)
- Perpendicular to the incline: \(F_{\text{perpendicular}} = Mg \cos \theta\)

Given \(\theta = 30^\circ\):
- \(F_{\text{parallel}} = Mg \sin 30^\circ = Mg \cdot \frac{1}{2} = \frac{Mg}{2}\)
- \(F_{\text{perpendicular}} = Mg \cos 30^\circ = Mg \cdot \frac{\sqrt{3}}{2} = \frac{Mg\sqrt{3}}{2}\)

Step 3: Calculate the normal force
The normal force \(N\) is equal to the perpendicular component of the gravitational force:
\( N = F_{\text{perpendicular}} = Mg \cos 30^\circ = \frac{Mg\sqrt{3}}{2} \)

Step 4: Calculate the frictional force
The frictional force can be calculated using the coefficient of friction (\(\mu\)):
\( f = \mu N = 0.3 \cdot N = 0.3 \cdot \frac{Mg\sqrt{3}}{2} = \frac{0.3Mg\sqrt{3}}{2} \)

Step 5: Write the equation of motion
The net force acting on the body along the incline is given by:
\( F_{\text{net}} = F_{\text{parallel}} - f \)
Substituting the values we found:
\( F_{\text{net}} = \frac{Mg}{2} - \frac{0.3Mg\sqrt{3}}{2} \)

Step 6: Factor out \(M\) and simplify
Factoring out \(M\) from the equation:
\( F_{\text{net}} = \frac{M}{2} \left( g - 0.3g\sqrt{3} \right) \)

Step 7: Calculate acceleration
Using Newton's second law, \(F = ma\), we can express acceleration \(a\) as:
\( a = \frac{F_{\text{net}}}{M} = \frac{1}{2} \left( g - 0.3g\sqrt{3} \right) \)
Substituting \(g = 10 \, \text{m/s}^2\):
\( a = \frac{1}{2} \left( 10 - 0.3 \cdot 10 \cdot \sqrt{3} \right) \)
Calculating \(0.3 \cdot 10 \cdot \sqrt{3} \approx 5.196\):
\( a = \frac{1}{2} \left( 10 - 5.196 \right) \approx \frac{1}{2} \cdot 4.804 \approx 2.402 \, \text{m/s}^2 \)

Final Answer
The acceleration of the body is approximately \(2.4 \, \text{m/s}^2\).

---