The force acting on a 4gm mass in the potential field U=8x2atx=−2cm is :
8 dyne
4 dyne
16 dyne
32 dyne
The correct Answer is:D
Step by step video, text & image solution for The force acting on a 4gm mass in the potential field U= 8x^2 at x= -2 cm is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - A Previous Year Problems | NEET
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -3 Section - B Previous Year Problems | JEE MAIN
23 Videos
- SIMPLE HARMONIC MOTIONBOOK - MOTIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - EXERCISE -1 (Objective Problems | NEET) SECTION-E Simple Pendulum
6 Videos
- SEMI CONDUCTOR AND LOGIC GATESBOOK - MOTIONCHAPTER - SEMI CONDUCTOR AND LOGIC GATESEXERCISE - EXERCISE 3
34 Videos
- SIMPLE HARONIC MOTION BOOK - MOTIONCHAPTER - SIMPLE HARONIC MOTION EXERCISE - EXERCISE -4 (Leve-II) [ JEE 2011]
11 Videos
Similar Questions
A conservative force acts on a 4 kg particle in x direction. The potential energy U(x) is given by U(X)=40+(x–6)2, where x is in metre. If it is given that at x = 8 m, KE is 30 J then find the maximum KE of the particle.
View SolutionA conservative force F(x) act on a 1kg particle. The potential energy U(x)=(x−4)2 , At x=5 ,particle has kinetic energy of 24J .The greatest value of x to which particle can move is
View Solution
Knowledge Check
A particle of mass 100 gm moves in a potential well given by U=8x2−4x+400 joule. Find its acceleration at a distance of 25 cm from equilibrium in the positive direction
A4ms−1B40ms−1C−40ms−1D−4ms−1The potnetial energy for a force field →F is given by U(x,y)=cos(x+y). The force acting on a particle at the position given by coordinates (0,π/4) is
A−1√2(ˆi+ˆj)B1√2(ˆi+ˆj)C(12ˆi+√32ˆj)D(12ˆi−√32ˆj)A particle is executing SHM with amplitude A. At displacement x=(−A4), force acting on the particle is F, potential energy of the particle is U, velocity of particle is v and kinetic energy is K. Assuming potential energyh to be zero at mean position. At displacement x=A/2
AForce acting on the particle will be 2FBpotential energy of the particle will be 4U.Cvelocity of particle must be √45vDkinetic energy of particle will be 0.8 K
A particle of mass 4 gm. Lies in a potential field given by V=200x2+150 ergs/gm. Deduce the frequency of vibration.
View SolutionA 2.00 kg particle moves along an x axis in onedimensional motion while a conservative force along that axis acts on it. The potential energy U(x) associated with the force is plotted in Fig. 8-36a. That is, if the particle were placed at any position between x=0 and x=7.00m, it would have the plotted value of U. At x=6.5m, the particle has velocity →v0=(−4.00m/s)ˆi.
(c) Evaluate the force acting on the particle when it is in the region 1.9 m<x<4.0 m.
View SolutionFigure given below shows the variation of potential energy function U(x), corresponding to a particle lying in a one dimensional force field. The force acting on the particle at x = 2 m is:
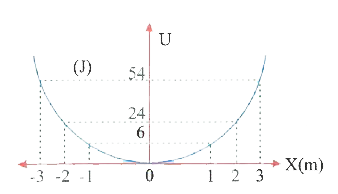
View SolutionThe potential energy for a force filed →F is given by U(x,y)=cos(x+y). The force acting on a particle at position given by coordinates (0,π/4) is
View SolutionIf x,F and U denote the dispalcement, force acting on and potential energy of a particle then
View Solution
