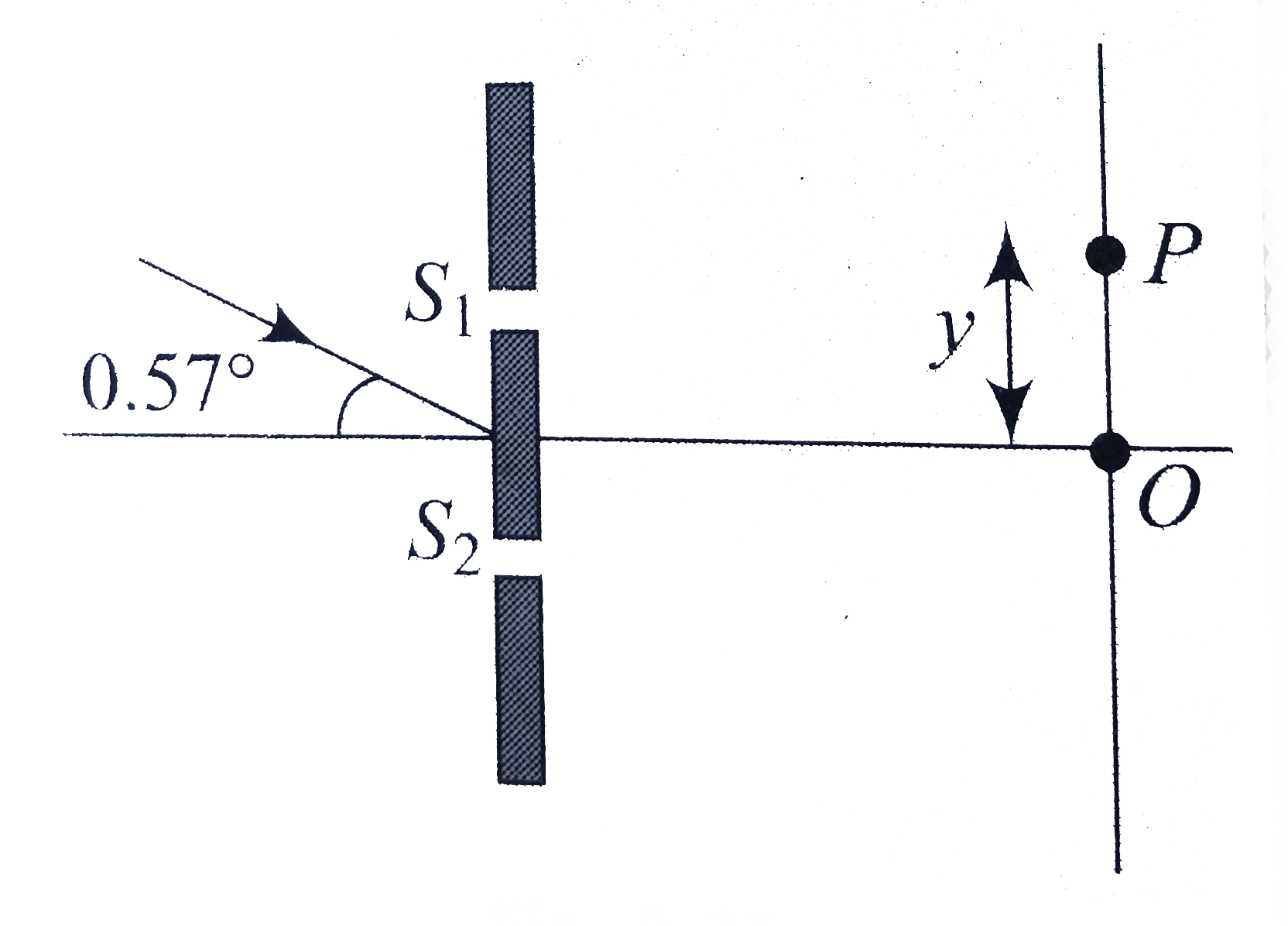
In YDSE with D=1m,d=1mm, light of wavelength 500nm is incident at an angle of 0.57∘ w.r.t. the axis of symmetry of the experimental set-up. If center of symmetry of screen is O as shown figure.
a. find the position of centrla maxima,
b. find intensity at point O in terms of intensity of central maxima I0, and
c. find number of maixma lying central maxima.
 .
.
(i) θ=θ0=57∘
⇒y=−Dtanθ≈
−Dθ=−1meter×(0.5757rad)
⇒y=−1cm
(ii) for point 0, θ=0
Hence, Δp=dsinθ0,
dθ0=1mm×(10−2rad)
=10,000nm
=20×(500nm)
⇒Δp=20λ
Hence point O corresponds to 20 th maxima
⇒ intensity at O=I0
(iii) 19 maxima lie between central maxima and O, excluding maxima at O and central maxima
Similar Questions
Light of wavelength 580 nm is incident on a slit having a width of 0.300 nm The viewing screen is 2.00 m from the slit. Find the positions of the first dark fringe and the width of the central bright fringe.
View SolutionLight of wavelength 6000Å is incident normally on single slit of width 0.23 mm. Find the angular spread between the central maxima and second-order maxima of diffraction pattern.
View Solution
Knowledge Check
Light of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is
A6×10−3 radB4×10−3 radC2.4×10−3 radD4.5×10−3 radThe light of wavelength 6328Å is incident on a slit of width 0.2mm perpendicularly, the angular width of central maxima will be
A(a) 0.36∘B(b) 0.18∘C(c) 0.72∘D(d) 0.09∘In YDSE path difference at a point on screen is λ8 . Find ratio of intensity at this point with maximum intensity.
A0.853B0.533C0.234D0.123
Find the intensities of the first three secondary maxima in the single-slit diffraction pattern, measured relative to the intensity of the central maximum
View SolutionFind the ratio of the intensities of the secondary maxima to the intensity of the central maximum for the single slit Fraunhofer diffraction pattern.
View SolutionLight of wavelength 6000Å is incident normally on a single slit of width 0.03 mm. Find the width of the central maxima on the screen which is at a distance 1.5 m away from the slit. What will be the width if the apparatus is immersed in water of refractive index 1.33?
View SolutionIn YDSE of equal width slits, if intensity at the center of screen is I0, then intensity at a distance of β/4 from the central maxima is
View SolutionIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
View Solution
