Find the electrostatic energy stored in a cylindrical shell of length I, inner radius a and outer radius b, coaxial with a uniformly charged wire with linear charge density .
For this we consider an elemental shell of radius x and width dx. The volume of this shell dV can be given as
The electric field due to the wire at the shell is
The electrostatic field energy stored in the volume of this shell is
or
The total electrostatic energy stored in the above mentioned volume can be obtained by integrating the above expression within limits from a to as
or
or
or
Topper's Solved these Questions
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise 1 (Section A-Questions Based on electric flux for various configuration, Question on solid angle concept, Gauss law Based Questions)
Explore 16 Videos
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise 1 (Section B - Properties of conductors)
Explore 15 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
Explore 13 Videos
- ERRORS , THEORY Book:MOTIONChapter:ERRORS , THEORY Exercise:EXERCISE 4 (LEVEL -II)
Explore 10 Videos
Similar Questions
In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
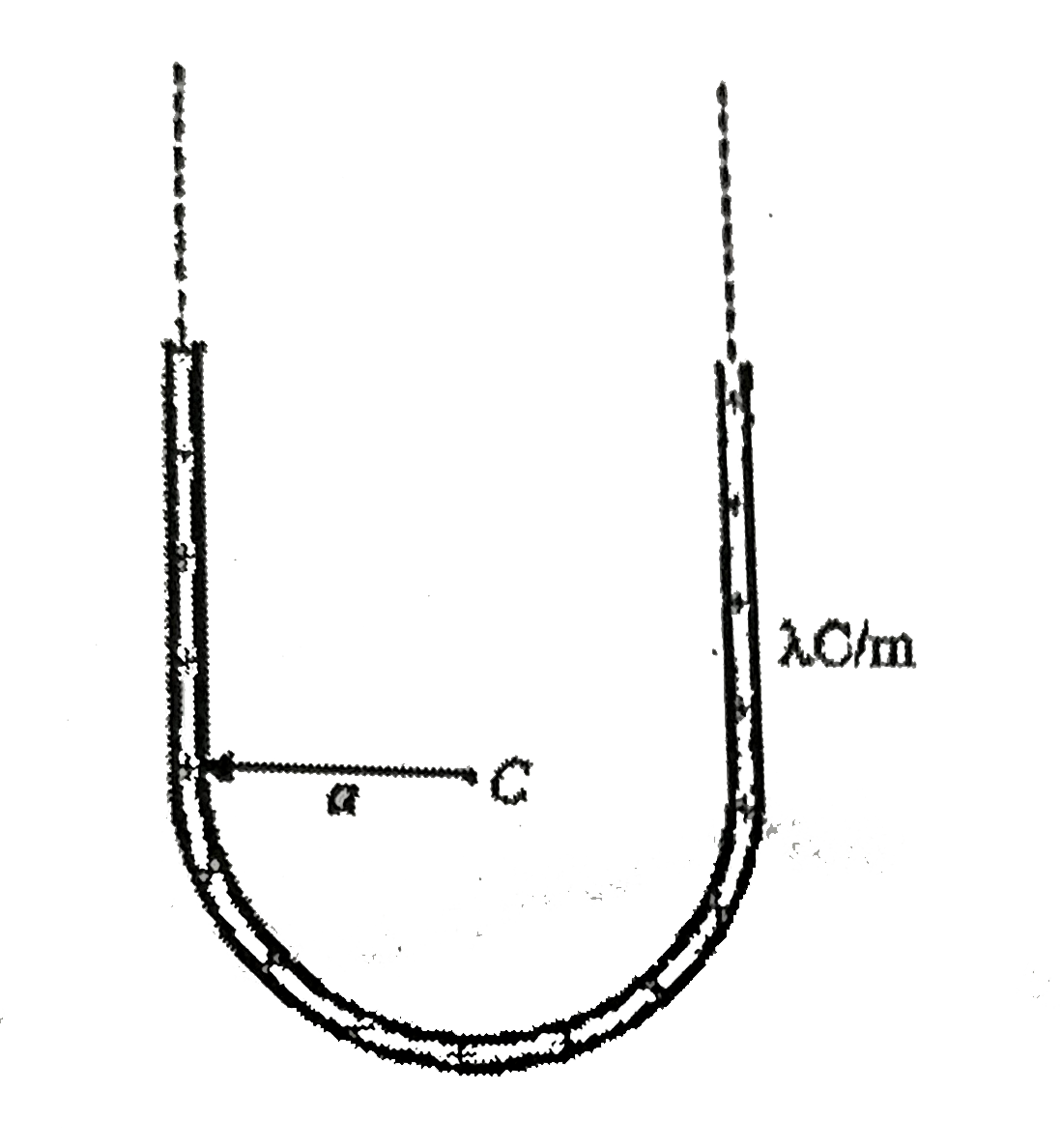
View SolutionA point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origen.
View Solution
Knowledge Check
Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
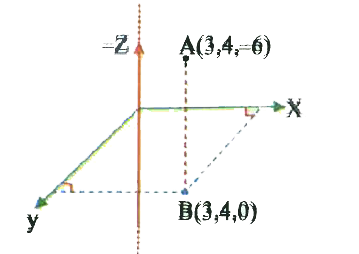 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1Two semicircular rings lying in same plane, of uniform linear charge density λ have radius r and 2r. They are joined using two straight uniformly charged wires of linear charge density λ and length r as shown in figure. The magnitude of electric field at common centre of semi circular rings is -
 A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λr
A14πε03λ2rB14πε0λ2rC14πε02λrD14πε0λrThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
AQ4πε0r for points outside and Q4πε0R for points inside the shellBQ4πε0e for both points inside nad outside the shellCzero for points outside and Q4πε0r for points inside the shellDzero for both points inside and outside the shell
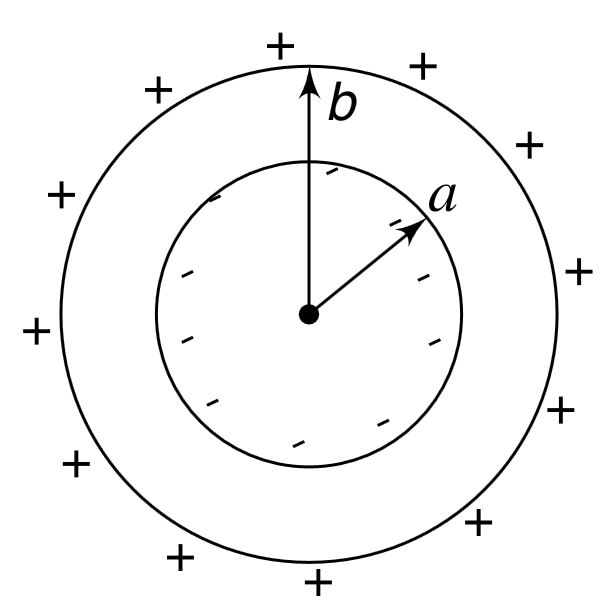
A thick conducting spherical shell of inner radius a and outer radius b is shown in figure. It is observed that the inner face of the shell carries a uniform charge density −σ. The outer surface also carries a uniform surface charge density +σ.
(a) Can you confidently say that there must be a charge inside the shell? Find the net charge present on the shell. (b) Find the potential of the shell.
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View SolutionAn infinitely long string uniformly charged with a linear charge density λ1=1μC/m and a segment of length I uniformly charged with linear charge density λ2=1ln4μ C/M lie in a plane at right angle to each other and separated by a distance lassbown∈thefigure.Determinetheforce (in mN ) with which these two intertct.
'(##CEN_KSR_PHY_JEE_C18_E01_035_Q20##)'
View SolutionA conducting spherical shell having inner radius a and outer radius b carries a net charge Q. If a point charge q is placed at the centre of this shell, then the surface charge density on the outer surface of the shell is given as:
View SolutionElectric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
View Solution
