In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density λ. [0]
![In the given arrangement find the electric field at C in the figure. Here the U-shaped wire is uniformly charged with linear charge density lambda. [0]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GAL_PHY_V03A_ECA_C01_E01_123_Q01.png)
The electric field due to the three parts of U-shaped wire are shown in figure (b). Thus we have
→Enet=(Ex1+Ex2)ˆi+(Ey1+Ey2+Ey3)ˆi
→Enet=(Eλa−Kλa)ˆi+(2Eλa−Eλa−Kλa)ˆj=0
Thus E.F. due to given arrangement at C = 0
Topper's Solved these Questions
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section A)
Explore 10 Videos
- ELECTROSTATICS - I Book:MOTIONChapter:ELECTROSTATICS - I Exercise:EXERCISE - 1 (Section B)
Explore 10 Videos
- ELECTROSTATICSBook:MOTIONChapter:ELECTROSTATICSExercise:Exercise -3 Section (B) Previous Year Problems | JEE Main
Explore 30 Videos
- ELECTROSTATICS-IIBook:MOTIONChapter:ELECTROSTATICS-IIExercise:Exercise - 4 (Level - II)
Explore 30 Videos
Similar Questions
Knowledge Check
The dimensional formula of linear charge density λ is
A[M−1L−1T+1A]B[M0L−1T+1A]C[M−1L−1T+1A−1]D[M0L−1T+1A−1]Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
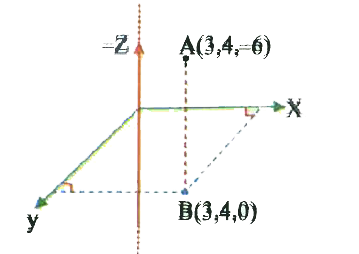 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
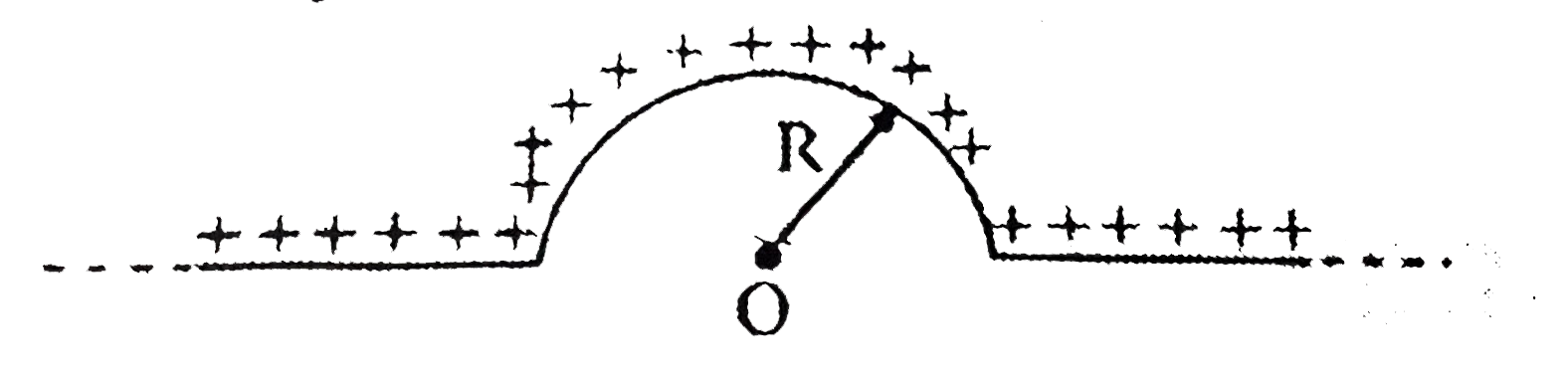 Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Aλ2πε0RBλ√22πε0RCλ√52πε0RDzero
Find the electric field at the centre of a semicircular ring if it is uniformly positive charged.
View SolutionUsing Gauss's law, derive an expression for the electric field intensity at any point near a uniformly charged thin wire of charge/length=λC/m.
View SolutionFind the electric field at the origin due to the line charge (ABCD) of linear charge density λ,

View Solution(a) There is an infinitely long thread uniformly charged with linear charge density λC/m. Using Gauss’ law, calculate the electric field (E0) at a distance x from the thread. (b) Now consider a semi-infinite uniformly charged thread (linear charge density =λ) as shown in figure. Find the y component of electric field at point P in terms of E0. Use simple qualitative argument. (c) For the situation described in (b) calculate the x component of electric field at point P using the method of integration. (d) Find the angle that the electric field at P makes with x direction.

View SolutionState Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density ) at a point lying at a distance r from the wire.
View Solution