Determine the maximum horizontal force F that may be applied to the plank of mass m for which the solid sphere does not slip as it begins to roll on the plank. The sphere has a mass M and radius R. The coefficient of static and kinetic friction between the sphere and the plank are μsandμk respectively.
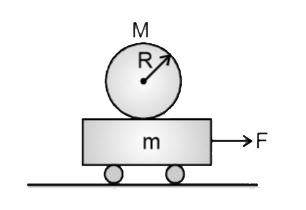
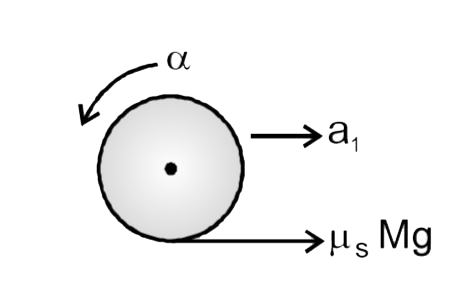
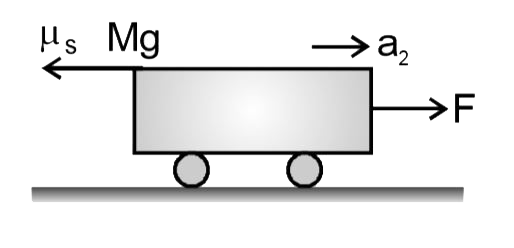
The free body diagrams of the sphere and the plank are as shown below :
Writing equations of motion :
For sphere : Linear acceleration
a1=μsMgM=μsg
Angular acceleration
α=(μsMg)R25MR2=52μsgR ...(ii) For plank : Linear acceleartion
a2=F−μsMgm ...(iii)
For no slipping acceleration of point B and A is same,
So: a2=a1+Rα
Solving the above four equation, we get
F=μsg(M+72m)
Thus, maximum value of F can be μsg(M+72m)

Topper's Solved these Questions
Similar Questions
A solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

Force of friction between sphere and plank is
View SolutionA solid sphere of mass m rolls without slipping on an inclined plain of inclination θ. What should be the minimum coefficient of static friction to support pure rolling?
View Solution
Knowledge Check
Chain of mass M length L kept on rough sphere. μ is coefficient if friction between sphere and chain F is minimum force required to slide chain
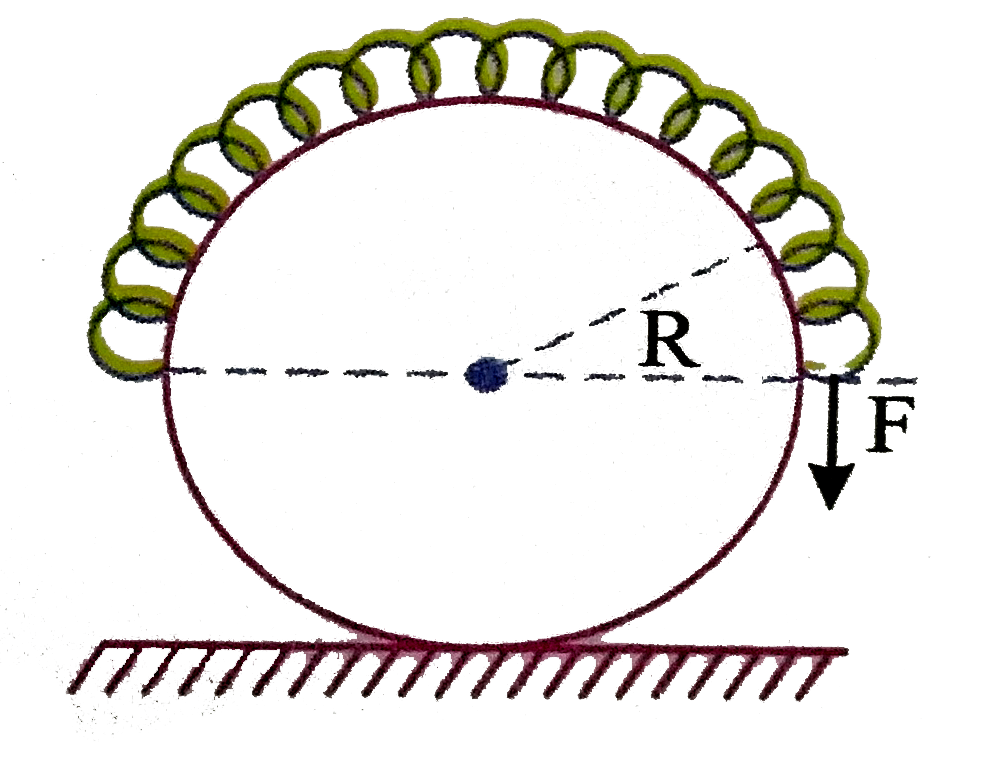 A2μMgπBμMgC<2μMgπD2μMg
A2μMgπBμMgC<2μMgπD2μMgA sphere of mass m and radius R is kept on a trolley of mass Mas shown in the figure. The coefficient of static and kinetic friction between the sphere and the trolley are μsandμk respectively. The maximum horizontal force F that can be applied to the trolley for which the solid sphere does not slip is
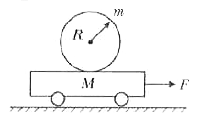 Aμsg(+72M)Bμkg(+72M)Cμsg(+52M)D92μsmg
Aμsg(+72M)Bμkg(+72M)Cμsg(+52M)D92μsmgA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isAF2BF4CF3D2F3
A plank of mass M is placed on a rough horizontal force F is applied on it A man of mass m rens on the plank find the acceleration of the man so that the plank does not move on the surface . The coefficent of friction between the plank and the surface is μ Assume that the man does not slip on the plank

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
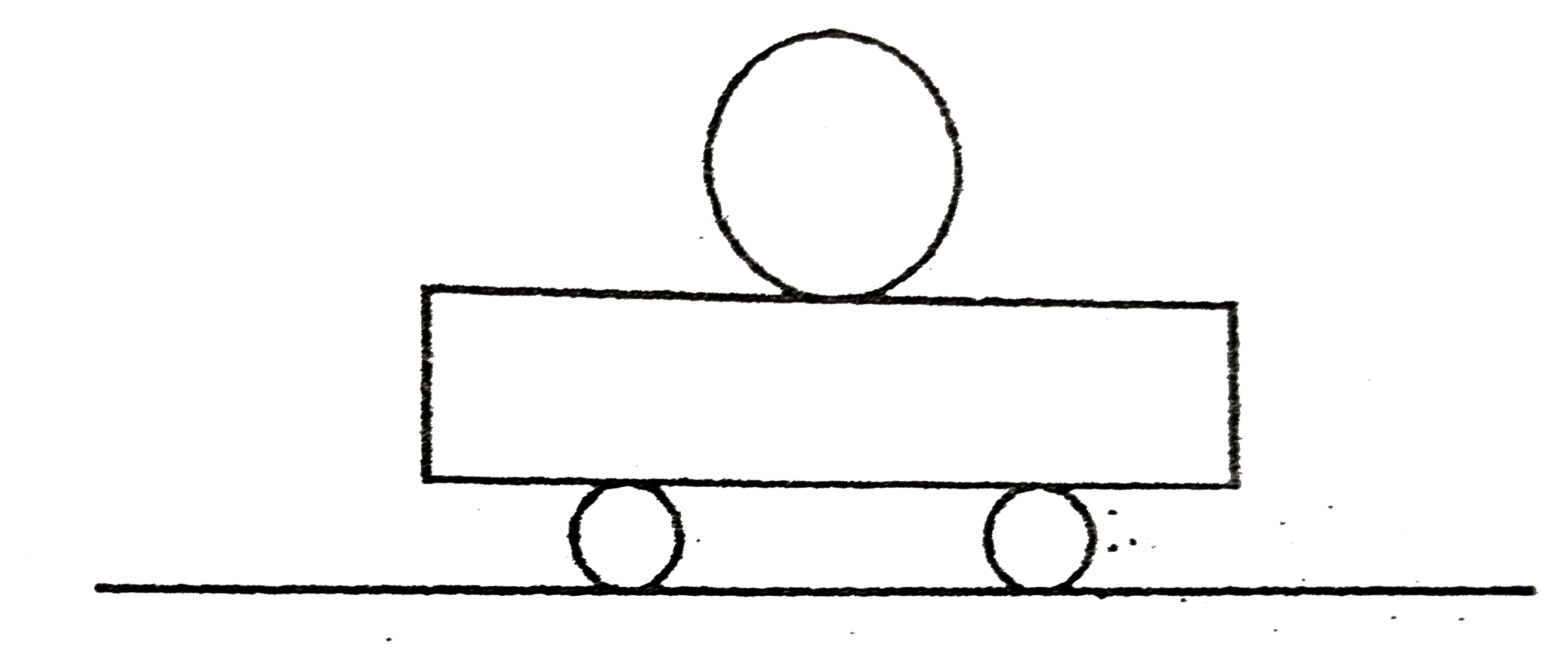
Angular acceleration of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA plank of mass m1 with a uniform solid sphere of mass m2 placed on it rests and a force F is applied to the plank. The acceleration of the plank provided there is no sliding between the plank and the sphere is (Fm1+n7m2) then the value of n is

View SolutionA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution

