Two blocks of masses 5kg and 10kg are attached with the help of light string and placed on a rough incline as shown in the figure. Coefficients of friction are as marked in the figure. The system is released from rest. Determine the acceleration of the two blocks.
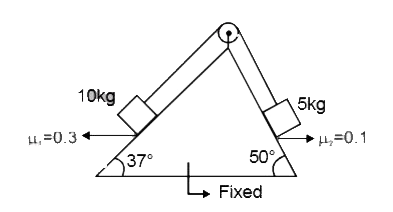
Let 10kg block is sliding down, then acceleration of both the bloks are given by,
a=10gsin37∘−μ1×10gcos37∘−5gsin50∘−μ2×5gcos50∘15=−ve
It means our assumed direction of motion is wrong and 5 kg block is going to slide down, if this would be the case, the direction of friction force will reverse and acceleration of blocks would be given by :
a1=5gsin50∘−μ2×5gcos50∘−μ1x10gcos37∘−10gsin37∘15=−ve
It means in this direction also there is no motion. So we can conclude that the system remains at rest and friction force is static in nature.
Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCIS-1
80 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2
66 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXAMPLE
47 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
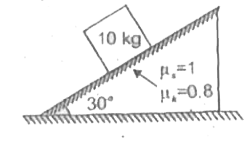
A block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
View SolutionTwo blocks of masses 4 kg and 2 kg are in contact with each other on an inclined plane of inclination 30∘ as shown in the figure . The coefficient of friction between 4 kg mass and the inclined plane is 0.3 , whereas between 2 kg mass and the plane is 0.2 . find the contact force between the blocks .

View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two discs A and B each of mass 2kg and radius 0.5m are rigidly fixed to the end of a thin shaft S, which is supported in horizontal position with the help of two smooth bearings at points P1 and P2. Two blocks of masses 2kg and 1kg are connected to the light cords wrapped around the discs as shown in the figure. There is no slipping between the cord and the discs. If the system is released from rest from the position shown, the mark released from rest from the position shown,
 APower developed by tension in cord connected to 2 kg block is negativeBAcceleration of each block is 2m/s2.CTotal work done by tension on discs is zero during the motion.DAcceleration of each block is 1m/s
APower developed by tension in cord connected to 2 kg block is negativeBAcceleration of each block is 2m/s2.CTotal work done by tension on discs is zero during the motion.DAcceleration of each block is 1m/sTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is
 A50N up the planeB50N down the planeC100N up the planeD100N down the plane
A50N up the planeB50N down the planeC100N up the planeD100N down the plane
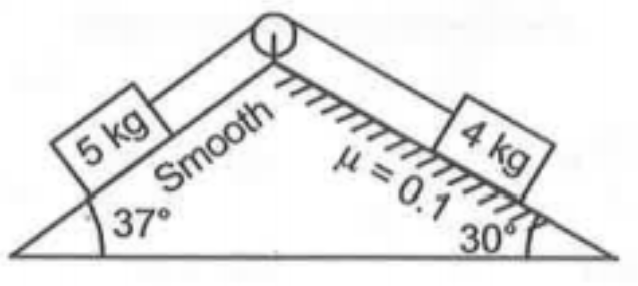
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
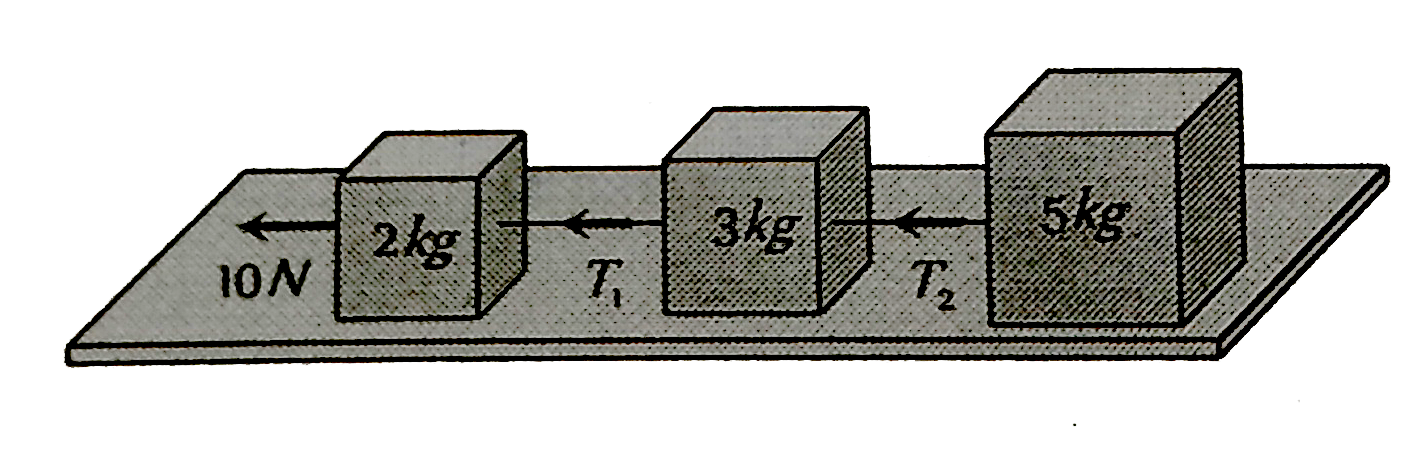
View SolutionThree blocks of masses 2 kg , 3 kg and 5 kg are connected to each other with light string and are then placed on a frictionless surface as shown in the figure. The system is pulled by a force F=10Nthen tension T1=
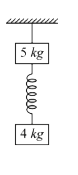
View SolutionTwo block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
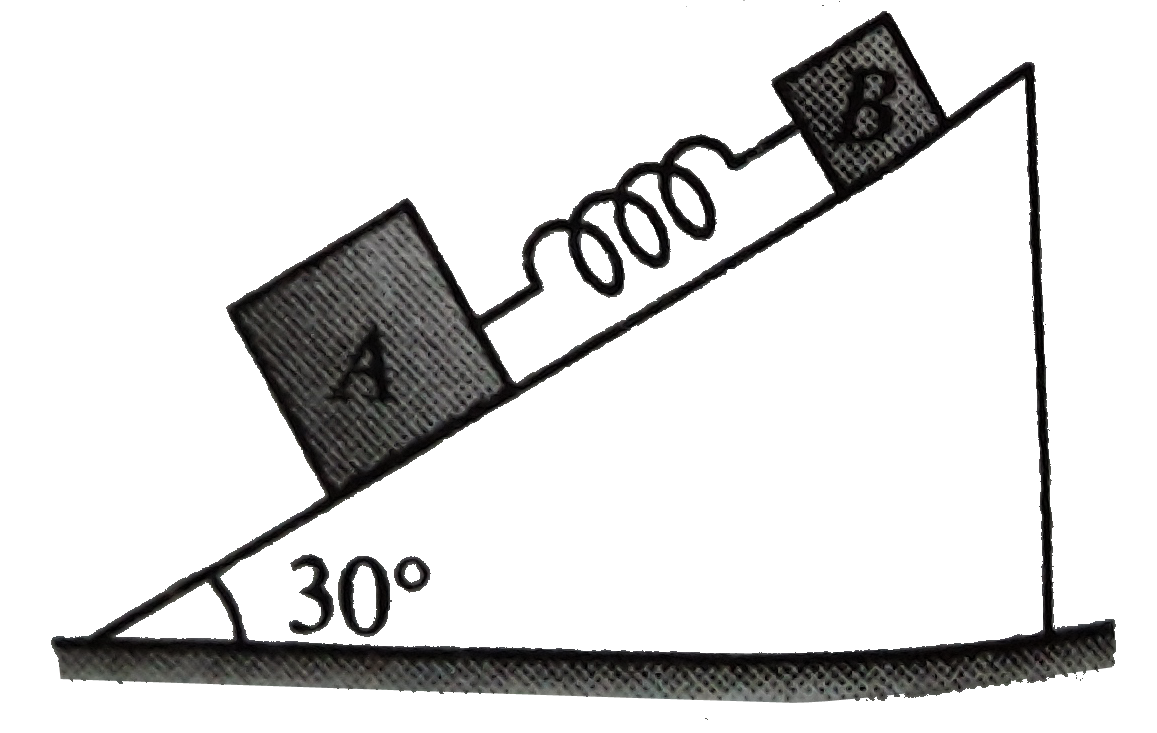
View SolutionTwo blocks A and B of masses 5kg and 2kg respectively connected by a spring of force constant =100Nm−1 are placed on an inclined plane of inclined 30∘ as shown in figure If the system is released from rest
View SolutionTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
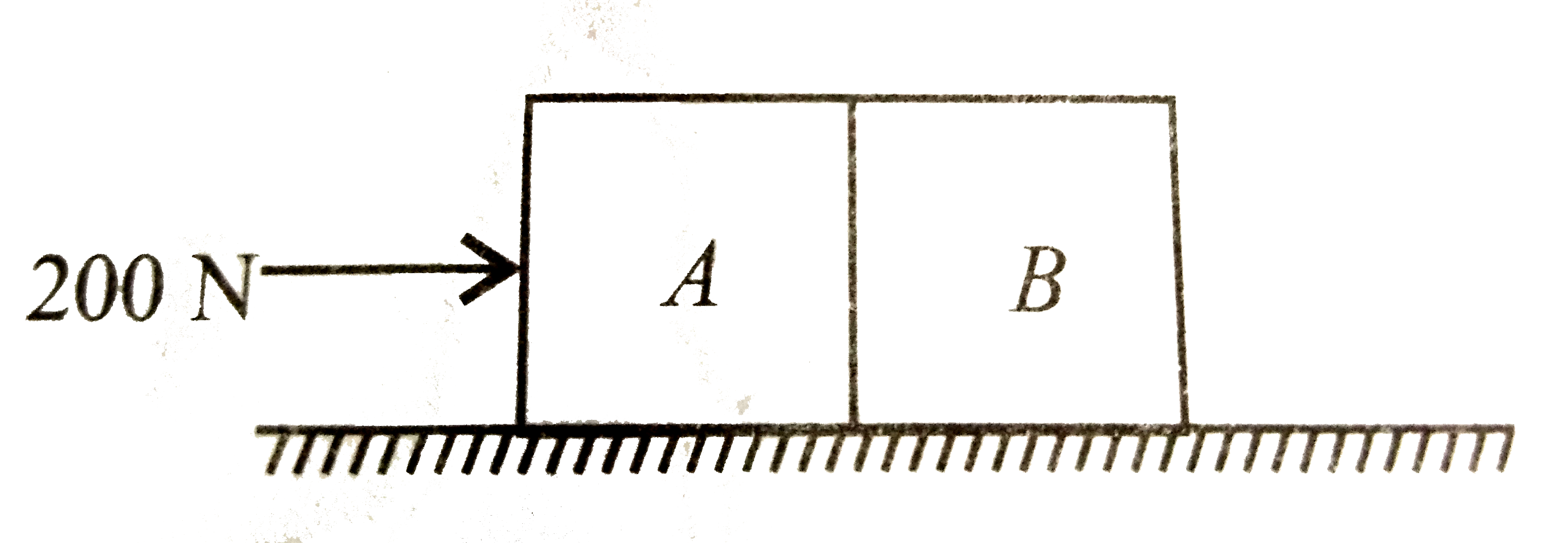
View Solution
