Find the accelerations of blocks A and B for the following cases.
(A) μ1=0 and μ2=0.1 (P)aA=aB=9.5m/s2
(B) μ2=0 and μ1=0.1 (Q)aA=9m/s2,aB=10m/s2
(C) μ1=0.1 and μ2=1.0 (R)aA=aB=g=10m/s2
(D) μ1=1.0 and μ2=0.1 (S)aA=1,aB=9m/s2
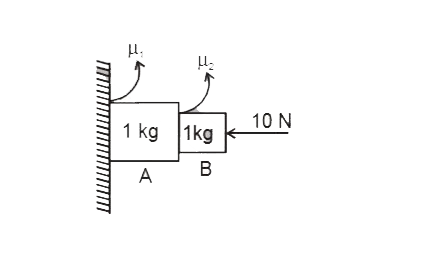
The correct Answer is:(a) R, ( b) Q, ( c ) P, (d) S
(i) FBD in ( case (i))
{μ1=0,μ2=0.1}
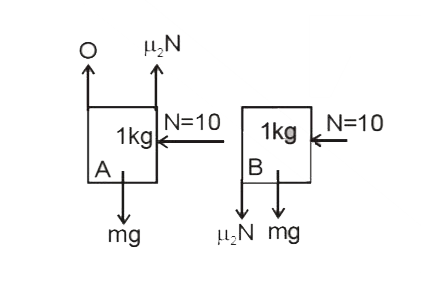
While friction's work is to oppose the relative motion and here if relative motion will start then friction comes and without relative motion there is no friction so both the block move together with same acceleration and friction will not come.
Friction between wall and block A oppose relative motion since wall is stationary so friction wants to slop block A also and maximum friction will act between wall and block while there is no friction between block.
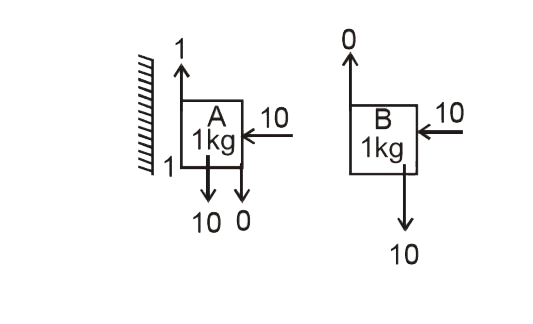
(iii) 
Friction between wall and block will be applied maximum equal to 1N but maximum friction available between block A and B is 10N but if this will be there then relative motion will increase while friction is to oppose relative motion. So friction will come less than 10 so friction will be f that will be static.

by system (20−1)=2×a
⇒a=192=9.5m/s2
(iv) aA=11−101=1m/s2
aB=10−11=9m/s2

Topper's Solved these Questions
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCIS-1
80 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-2
66 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXAMPLE
47 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 3 Section-B
12 Videos
- ONE DIMENSION MOTIONBOOK - MOTIONCHAPTER - ONE DIMENSION MOTIONEXERCISE - Exercise - 3 |Section - B Previous Year Problems | JEE MAIN
12 Videos
Similar Questions
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0 , then the value of c is
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0, then the value of 'c' is:
View Solution
Knowledge Check
If the equation of the locus of a point equidistant from the points (a1,b1, and (a2,b2) is
(a1−a2)x+(b1−b2)y+c=0, then the value of c isA12(a22+b22)−(a21−b21)B(a21−a22+b21−b22)C12(a21+a22+b21+b22)D√(a21+b21−a22−b22)The equation of a plane containning the lines r=a1+t b1andr=a2+t b2, where [(a2−a1)b1b2]=0 is
A[(r+a1)⋅(b1×b2)]=1B[(r−b1)⋅a⋅(b1×b2)]=0C[(r−a1)⋅(b1×b2)]=0DNone of theseIn which of the following cases the friction force between 'A' and 'B' is maximum. In all cases μ1=0.5,μ2=0.
A B
B C
C D
D
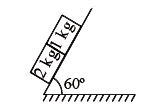
In the figure shown, if friction coefficient of block 1 kg and 2kg with inclined plane is μ1=0.5 and μ2=0.4 respectively, then
View SolutionIf the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a−1−a2)x+(b1−b2)y+c=0 , then the value of c is
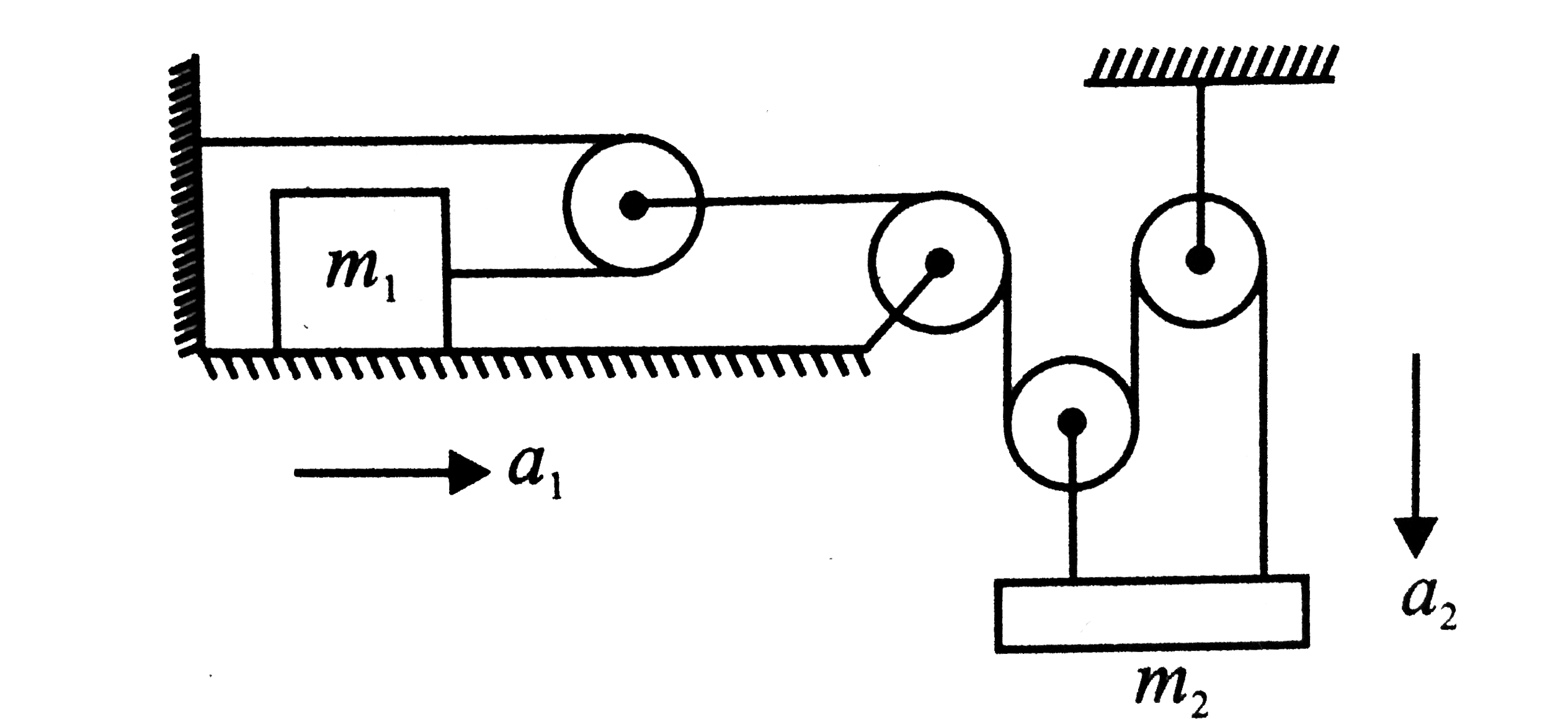
View SolutionTwo blocks are arranged as shown in figure. Find the ratio of a1/a2. (a1 is acceleration of m1 and a2 that of m2)
View SolutionIf A1 and A2 are two A.M.'s between a and b, prove that
(i) (2A1−A2)(2A2−A1)=ab
(ii) A1+A2=a+b
View SolutionIf the ratio of the roots of a1x2+b1x+c1=0 be equal to the ratio of the roots of a2x2+b2+c2=0, then a1a2,b1b2,c1c2 are in
View Solution
