Three identical spheres each of radius R are placed touching side by side along X axis so that the centre of the first sphere is at the origin. Now the sphere at the extreme end is removed. The shift in the centre of mass is (A) R (B) 2R (C) R 2 (D) 3R
Step by step video & image solution for Three identical spheres each of radius R are placed touching side by side along X axis so that the centre of the first sphere is at the origin. Now the sphere at the extreme end is removed. The shift in the centre of mass is (A) R (B) 2R (C) R 2 (D) 3R by Physics experts to help you in doubts & scoring excellent marks in Class 13 exams.
Updated on:21/07/2023Similar Questions
Three identical spheres each of radius 'R' are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is.
View SolutionThree identical spheres each of radius 3cm are placed on a horizontal surface touching one another. The distance of centre of mass of system from any centre of the sphere is
View Solution
Knowledge Check
Three identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
A2R3B2RC5R3D4R3Three identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
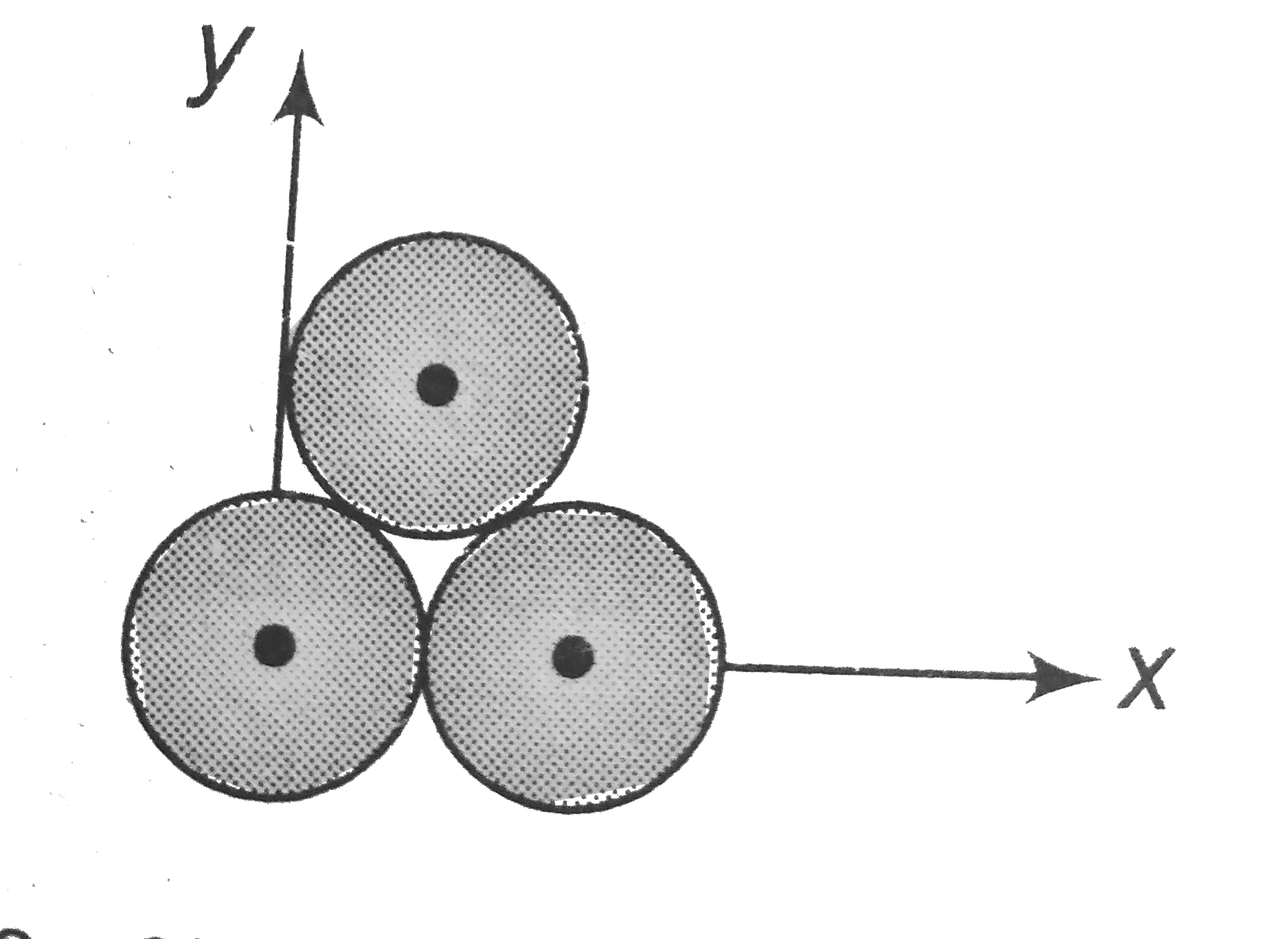 .A(R,R)B(0,0)C(R2,R2)D(R,R√3)
.A(R,R)B(0,0)C(R2,R2)D(R,R√3)The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4r
A solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View SolutionTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
View SolutionA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
View Solution
