A solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
To find the distance of the center of mass from the interface between a solid sphere and a cube, we will follow these steps:
Step 1: Identify the dimensions and masses
- The radius of the sphere R.
- The side length of the cube 2R.
- Both objects are made of the same material, so they have the same density ρ.
Step 2: Calculate the mass of the sphere
The mass Ms of the sphere can be calculated using the formula for the volume of a sphere and multiplying it by the density:
Ms=Volume of sphere×Density=43πR3ρ
Step 3: Calculate the mass of the cube
The mass Mc of the cube can be calculated using the formula for the volume of a cube and multiplying it by the density:
Mc=Volume of cube×Density=(2R)3ρ=8R3ρ
Step 4: Identify the center of mass positions
- The center of mass of the sphere is located at a distance R above the interface (top of the cube).
- The center of mass of the cube is located at its geometric center, which is at a distance R below the top face (the interface).
Step 5: Set up the coordinate system
- Let the interface be at y=0.
- The center of mass of the sphere is at y=R (above the interface).
- The center of mass of the cube is at y=−R (below the interface).
Step 6: Calculate the center of mass of the system
Using the formula for the center of mass ycm:
ycm=Msys+McycMs+Mc
Where:
- ys=R (position of the sphere's center of mass)
- yc=−R (position of the cube's center of mass)
Substituting the masses:
ycm=(43πR3ρ⋅R)+(8R3ρ⋅(−R))43πR3ρ+8R3ρ
Step 7: Simplify the equation
Calculating the numerator:
=43πR4ρ−8R4ρ
Calculating the denominator:
=43πR3ρ+8R3ρ
Step 8: Factor out common terms
Factoring out R4ρ from the numerator and R3ρ from the denominator:
ycm=R4ρ(43π−8)R3ρ(43π+8)
This simplifies to:
ycm=R⋅43π−843π+8
Step 9: Interpret the result
Since 43π is approximately 4.19, which is less than 8, the numerator will be negative, indicating that the center of mass is below the interface.
Final Result
Thus, the distance of the center of mass from the interface is:
ycm=R⋅43π−843π+8
- The radius of the sphere R.
- The side length of the cube 2R.
- Both objects are made of the same material, so they have the same density ρ.
The mass Ms of the sphere can be calculated using the formula for the volume of a sphere and multiplying it by the density:
Ms=Volume of sphere×Density=43πR3ρ
The mass Mc of the cube can be calculated using the formula for the volume of a cube and multiplying it by the density:
Mc=Volume of cube×Density=(2R)3ρ=8R3ρ
- The center of mass of the sphere is located at a distance R above the interface (top of the cube).
- The center of mass of the cube is located at its geometric center, which is at a distance R below the top face (the interface).
- Let the interface be at y=0.
- The center of mass of the sphere is at y=R (above the interface).
- The center of mass of the cube is at y=−R (below the interface).
Using the formula for the center of mass ycm:
ycm=Msys+McycMs+Mc
Where:
- ys=R (position of the sphere's center of mass)
- yc=−R (position of the cube's center of mass)
ycm=(43πR3ρ⋅R)+(8R3ρ⋅(−R))43πR3ρ+8R3ρ
Calculating the numerator:
=43πR4ρ−8R4ρ
Calculating the denominator:
=43πR3ρ+8R3ρ
Factoring out R4ρ from the numerator and R3ρ from the denominator:
ycm=R4ρ(43π−8)R3ρ(43π+8)
This simplifies to:
ycm=R⋅43π−843π+8
Since 43π is approximately 4.19, which is less than 8, the numerator will be negative, indicating that the center of mass is below the interface.
Thus, the distance of the center of mass from the interface is:
ycm=R⋅43π−843π+8
Similar Questions
A solid sphere of radius r is melted and recast into the shape of a solid cone of height r. Find radius of the base of the cone.
View SolutionA disc of radius R is placed on a square plate of edge 4R made up of the same sheet with their planes parallel such that any two adjacent sides ofsquare touch the disc. Find the distance of the centre of mass of the system from the centre of square plate?
View Solution
Knowledge Check
A solid hemisphere and a solid cone have a common base and are made of same material. The centre of mass of the common structure coincides with the centre of the common base. If R is the radius of hemisphere and h is height of the cone, then
 AhR=√3BhR=1√3ChR=3DhR=13
AhR=√3BhR=1√3ChR=3DhR=13A circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
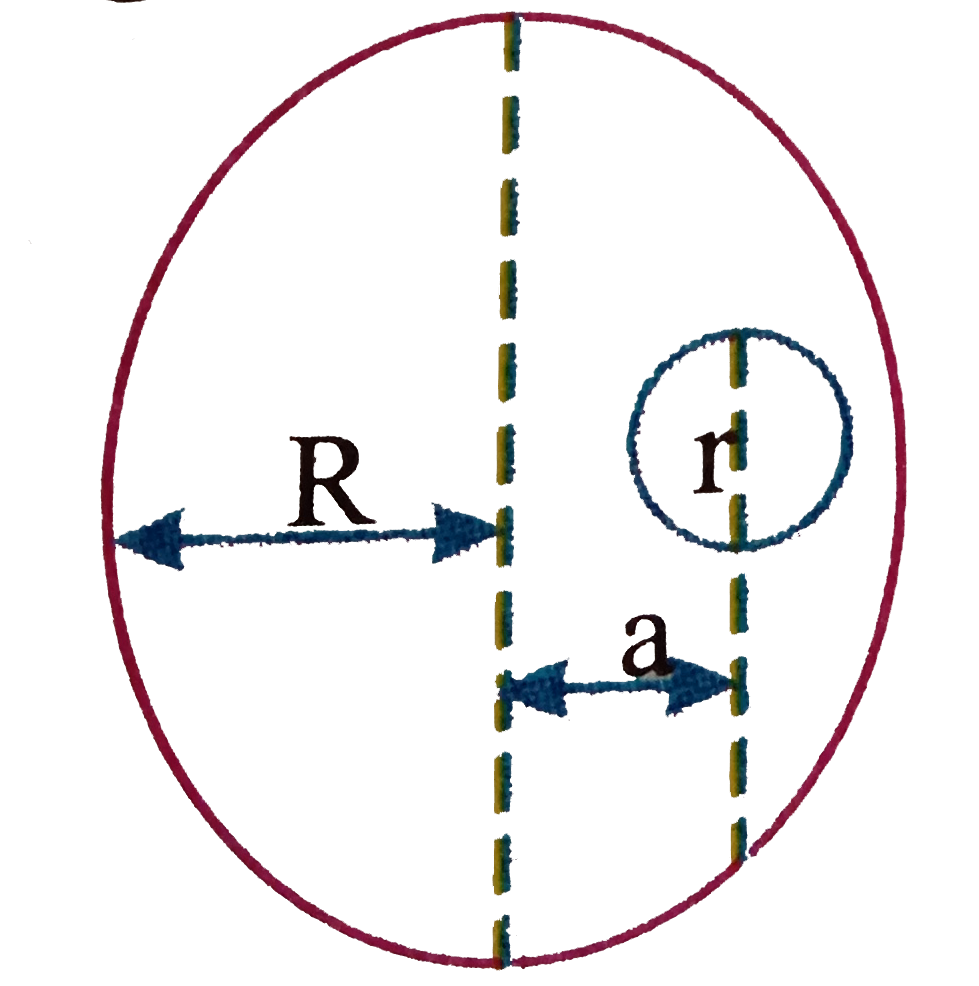 AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is
 AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
AYCM=−R15BYCM=−R40CYCM=−R30DYCM=−R20
A solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionAn isolated solid metal sphere of radius R is given an electric charge. The variation of the intensity of the electric field with the distance r from the centre of the sphere is best shown by
View SolutionA solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution

