Three identical spheres each of mass m and radius R are placed touching each other so that their centres A,B and C lie on a straight line. The position of their centre of mass from centre of A is
2R3
2R
5R3
4R3
The correct Answer is:B
To find the position of the center of mass of three identical spheres, each with mass m and radius R, placed touching each other in a straight line, we can follow these steps:
1. Identify the Positions of the Centers:
- Let the center of the first sphere (Sphere A) be at the origin, A(0,0).
- The center of the second sphere (Sphere B) will be at a distance of 2R from Sphere A, so its position is B(2R,0).
- The center of the third sphere (Sphere C) will be at a distance of 2R from Sphere B, making its position C(4R,0).
2. Use the Center of Mass Formula:
The formula for the center of mass xcm of a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
Here, m1=m2=m3=m, and the positions are x1=0, x2=2R, and x3=4R.
3. Substitute the Values:
xcm=m⋅0+m⋅2R+m⋅4Rm+m+m
Simplifying this:
xcm=0+2mR+4mR3m=6mR3m=2R
4. Determine the Position Relative to Sphere A:
The center of mass is located at 2R from the origin (center of Sphere A). Since the center of Sphere A is at 0, the center of mass is 2R away from Sphere A.
Final Answer:
The position of the center of mass from the center of Sphere A is 2R.
---
- Let the center of the first sphere (Sphere A) be at the origin, A(0,0).
- The center of the second sphere (Sphere B) will be at a distance of 2R from Sphere A, so its position is B(2R,0).
- The center of the third sphere (Sphere C) will be at a distance of 2R from Sphere B, making its position C(4R,0).
The formula for the center of mass xcm of a system of particles is given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
Here, m1=m2=m3=m, and the positions are x1=0, x2=2R, and x3=4R.
xcm=m⋅0+m⋅2R+m⋅4Rm+m+m
Simplifying this:
xcm=0+2mR+4mR3m=6mR3m=2R
The center of mass is located at 2R from the origin (center of Sphere A). Since the center of Sphere A is at 0, the center of mass is 2R away from Sphere A.
The position of the center of mass from the center of Sphere A is 2R.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-II(C.W.)
Explore 64 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-III
Explore 66 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:C.U.Q.
Explore 83 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
Determine the position of the centre of mass of a hemisphere of radius R.
View SolutionThree identical spheres each of mass M and radius R are arranged in a row touching each other and their centres collinear.The moment of inertia of the system about an axis passing through the centre of the middle sphere and perpendicular to the line joining their centres is "
View Solution
Knowledge Check
Three identicle particle each of mass 1kg are placed with their centres on a straight line. Their centres are marked A,BandC respectively. The distance of centre of mass of the system from A is.
AKL+KM+LM3BKL+KM3CKL+LM3DKM+LM3Three identical spheres each of radius R are placed touching each other on a horizontal table as shown in figure. The co-ordinates of centre of mass are :
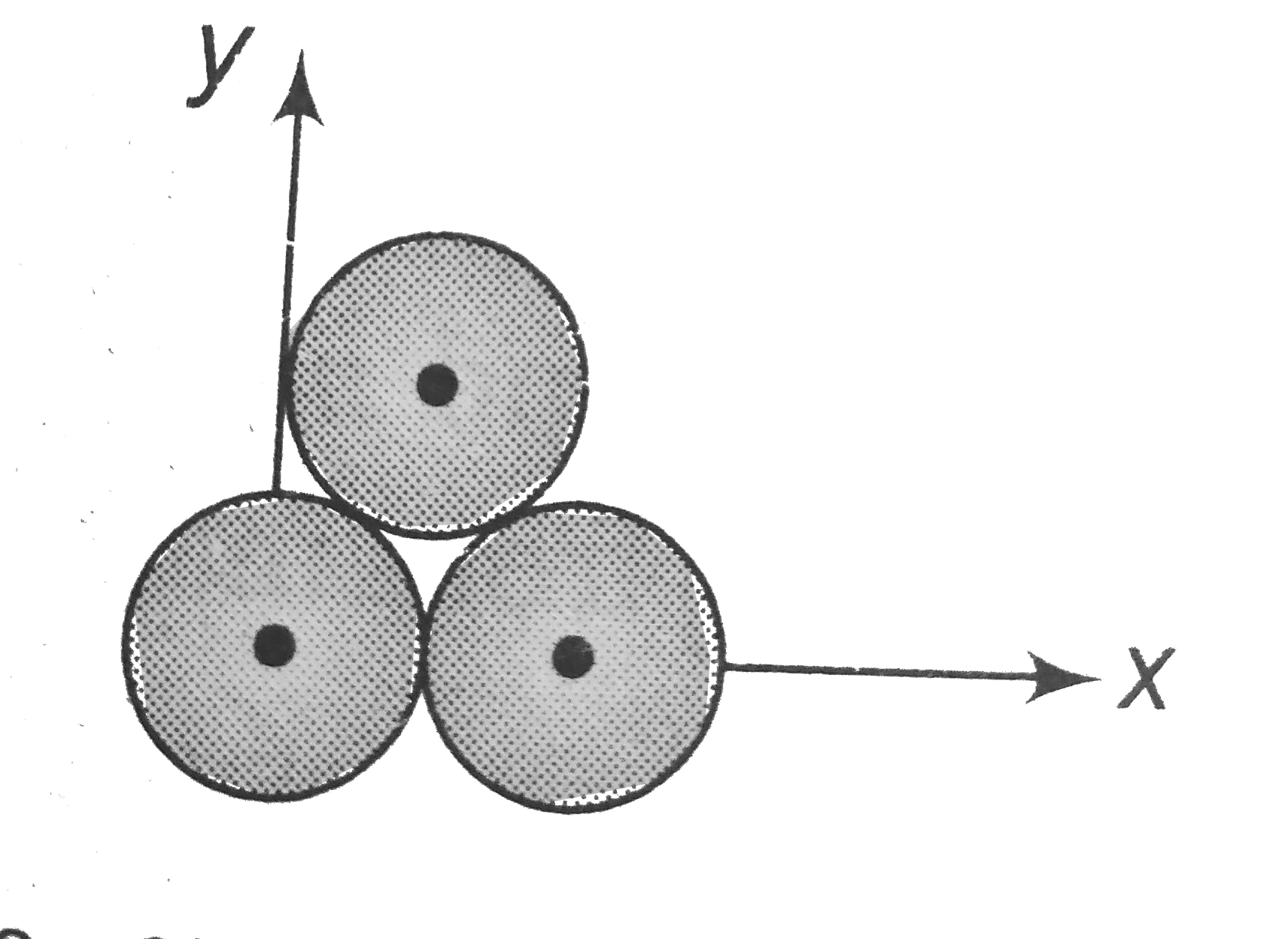 .A(R,R)B(0,0)C(R2,R2)D(R,R√3)
.A(R,R)B(0,0)C(R2,R2)D(R,R√3)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
Three identical particles each of same mass are placed touching each other with their centres on a straight line.Their centres are at A,B,and C respectively.Then distance of centre of mass of the system from A is
View SolutionThree identical spheres, each of mass 1 kg are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked P, Q, R respectively, the distance of centre of mass of the system from P (origin) is
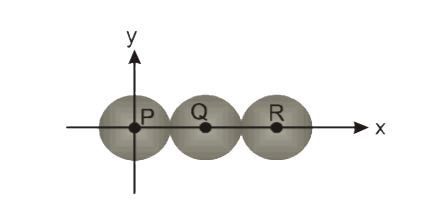
View SolutionFour identical bodies each of mass 1 kg are placed touching to each other with centres on a straight line. If their centres are marked A, B, C and D respectively, then the distance of centre of mass of the system from B will be

View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View Solution

