Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
The correct Answer is:D
To find the position vector of the center of mass of three identical spheres placed at the corners of an equilateral triangle, we can follow these steps:
Step 1: Define the positions of the spheres
Let's denote the three spheres located at the corners of an equilateral triangle with side length 2 m. We will place one corner at the origin (0, 0) and define the positions of the other two corners based on this.
1. Sphere 1 (at origin):
- Position vector r1=(0,0)
2. Sphere 2 (2 m along the x-axis):
- Position vector r2=(2,0)
3. Sphere 3 (at the third corner):
- To find the coordinates of the third sphere, we can use the properties of an equilateral triangle. The height h of the triangle can be calculated using:
h=√32×side length=√32×2=√3
- The coordinates of Sphere 3 will be:
- Position vector r3=(1,√3) (1 m along the x-axis and √3 m along the y-axis).
Step 2: Calculate the center of mass
The formula for the center of mass Rcm of a system of particles is given by:
Rcm=m1r1+m2r2+m3r3m1+m2+m3
Since all spheres have the same mass M, we can simplify the equation:
Rcm=Mr1+Mr2+Mr3M+M+M=r1+r2+r33
Step 3: Substitute the position vectors
Substituting the position vectors into the formula:
Rcm=(0,0)+(2,0)+(1,√3)3
Calculating the sum:
Rcm=(0+2+1,0+0+√3)3=(3,√3)3=(1,√33)
Step 4: Write the final position vector
Thus, the position vector of the center of mass is:
Rcm=(1,√33)
Final Answer
The position vector of the center of mass is (1,√33).
---
Let's denote the three spheres located at the corners of an equilateral triangle with side length 2 m. We will place one corner at the origin (0, 0) and define the positions of the other two corners based on this.
- Position vector r1=(0,0)
- Position vector r2=(2,0)
- To find the coordinates of the third sphere, we can use the properties of an equilateral triangle. The height h of the triangle can be calculated using:
h=√32×side length=√32×2=√3
- The coordinates of Sphere 3 will be:
- Position vector r3=(1,√3) (1 m along the x-axis and √3 m along the y-axis).
The formula for the center of mass Rcm of a system of particles is given by:
Rcm=m1r1+m2r2+m3r3m1+m2+m3
Since all spheres have the same mass M, we can simplify the equation:
Rcm=Mr1+Mr2+Mr3M+M+M=r1+r2+r33
Substituting the position vectors into the formula:
Rcm=(0,0)+(2,0)+(1,√3)3
Calculating the sum:
Rcm=(0+2+1,0+0+√3)3=(3,√3)3=(1,√33)
Thus, the position vector of the center of mass is:
Rcm=(1,√33)
The position vector of the center of mass is (1,√33).
Topper's Solved these Questions
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - MHT CET Corner
35 Videos
- ROTATIONAL MOTION'BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ROTATIONAL MOTION'EXERCISE - PRACTICE EXERCISE (Exercise 1 (TOPICAL PROBLEMS))
70 Videos
- REFRACTION OF LIGHTBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 2
25 Videos
- SCALARS AND VECTORS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SCALARS AND VECTORS EXERCISE - Exercise 2 (Miscellaneous Problems)
20 Videos
Similar Questions
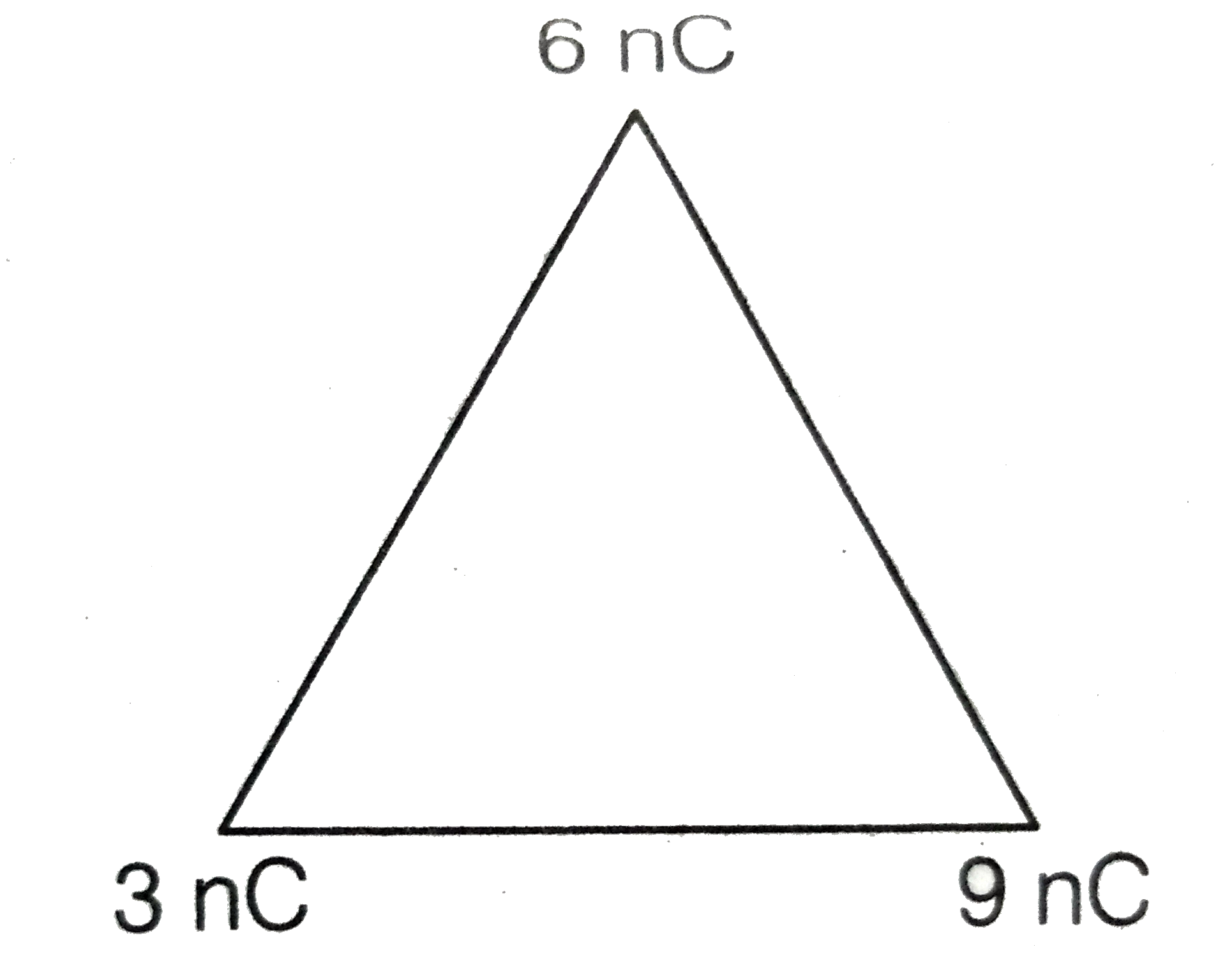
Three point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
View SolutionThree equal masses (each m) are placed at the corners of an equilateral triangle of side a. Then the escape velocity of an object from the circumcentre P of triangle is
View Solution
Knowledge Check
Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3Four identical spheres each of mass m are placed at the corner of square of side 2 m. Taking the point of intersection of the diagonals as the orgin the coordinates of the centre of mass are ?
A(0,0)B(1,1)C(-1,1)D(1,-1)
Three particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View SolutionThree particles each of mass 2kg are at the corners of an equilateral triangle of side √3m. If one of the particles is removed, the shift in the centre of mass is
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
View SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View Solution
