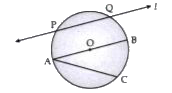
Consider a circles S with centre at the origin and radius 4. Four circles A, B, C and Deach with radiusunity and centres (−3,0),(−1,0),(1,0) and (3,0) respectively are drawn. A chord PQ of the circle Sne circle B and passes through the centre of the circle C. If the length of this chord can beexpressed as √x , find x.
The correct Answer is:63
Step by step video, text & image solution for Consider a circles S with centre at the origin and radius 4. Four circles A, B, C and Deach with radiusunity and centres (-3, 0), (-1,0), (1,0) and (3, 0) respectively are drawn. A chord PQ of the circle Sne circle B and passes through the centre of the circle C. If the length of this chord can beexpressed as sqrtx , find x. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBook:MOTIONChapter:CIRCLEExercise:Exercise - 3 (Subjective | JEE Advanced) Matrix Match Type
Explore 1 Video
- CIRCLEBook:MOTIONChapter:CIRCLEExercise:Exerise - 4 | Level - I (Previous Year|JEE Main
Explore 10 Videos
- CIRCLEBook:MOTIONChapter:CIRCLEExercise:Exercise -2 (Level - II) Multiple correct | JEE Advanced
Explore 14 Videos
- BINOMIAL THEOREM Book:MOTIONChapter:BINOMIAL THEOREM Exercise:Exercise -4 (Level - II) ( Previous Year )
Explore 7 Videos
- COMPLEX NUMBER Book:MOTIONChapter:COMPLEX NUMBER Exercise:EXERCISE - 4 (LEVEL -II) PREVIOUS YEAR - JEE ADVANCED
Explore 33 Videos
Similar Questions
Knowledge Check
A chord that passes through the centre of a circle is___
ADiameterBSegmentCRadiusDCentreThe chord of a circle which passes through the centre is___the radius
AThriceBDoubleCHalfDEqual toEquation of the circle with centre at (1,-2) , and passing through the centre of the circle x2+y2+2y−3=0 , is
Ax2+y2−2x+4y+3=0Bx2+y2−2x+4y−3=0Cx2+y2+2x−4y−3=0Dx2+y2+2x−4y+3=0
A chord PQ of a circle of radius 10 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major and the minor segment
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionA chord of length 30cm is drawn at a distance of 8 cm from the centre of a circle. Find out the radius of the circle.
View SolutionTwo circles with equal radii are intersecting at the points (1,0) and (−1,0). Then tangent at the point (1,0) to one of the circles passes through the centre of the other circle.Then the distance between the centres of these circles is:
View SolutionA variable chord is drawn through the origin to the circle x2+y2−2ax=0. The locus of the centre of the circle drawn on this chord as diameter is
View Solution