Question

If a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.

Explanation

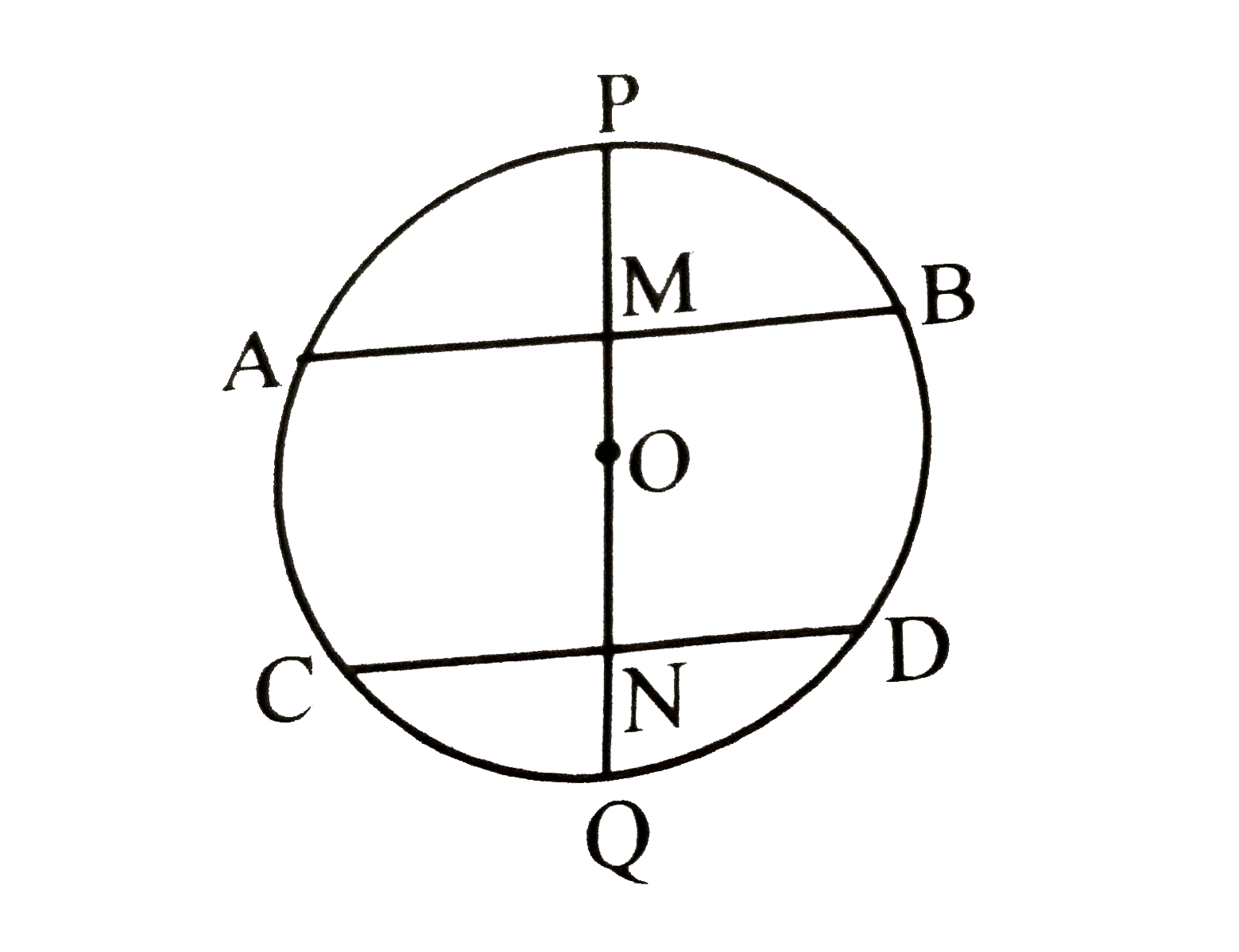
Given AB and CD are two chords of a circle whose centre is O and PQ is a diameter bisecting the chord AB and CD at L and M, respectively and the diameter PQ passes through the centre O of the circle.
To prove `AB||CD `
Proof Since, L is the mid-point of AB.
`:. OL bot AB`
[since, the line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord]
`rArr angle ALO=90^(@) ....(i)`
Similarly, `OM bot CD ...(ii)`
From Eqs. (i) and (ii) `angleALO=angleOMD=90^(@)`
But, these are alternating angles.
So, `AB||CD`