A chord PQ of a circle of radius 10 cm makes an angle of 60∘ at the centre of the circle. Find the area of the major and the minor segment
The correct Answer is:Minor segment = 9.08 cm2, major segment =305.20cm2
To solve the problem of finding the area of the major and minor segments of a circle with a radius of 10 cm and a chord PQ that makes an angle of 60° at the center, we can follow these steps:
Step 1: Calculate the Area of the Sector
The area of the sector formed by the angle at the center can be calculated using the formula:
Area of Sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
Here, θ=60∘ and r=10cm.
Area of Sector=60360×π×(10)2
=16×π×100
=100π6cm2
=50π3cm2
Step 2: Calculate the Area of the Triangle
Next, we need to find the area of triangle OPQ, where O is the center of the circle. The formula for the area of a triangle when two sides and the included angle are known is:
Area of Triangle=12×a×b×sin(C)
where a and b are the lengths of the sides and C is the included angle.
In this case, both sides (radii) are equal to 10 cm, and the angle C=60∘.
Area of Triangle=12×10×10×sin(60∘)
=12×100×√32
=25√3cm2
Step 3: Calculate the Area of the Minor Segment
The area of the minor segment can be calculated by subtracting the area of the triangle from the area of the sector:
Area of Minor Segment=Area of Sector−Area of Triangle
=50π3−25√3cm2
Step 4: Calculate the Area of the Major Segment
The area of the major segment can be found by subtracting the area of the minor segment from the total area of the circle:
Area of Circle=πr2=π(10)2=100πcm2
Area of Major Segment=Area of Circle−Area of Minor Segment
=100π−(50π3−25√3)
=100π−50π3+25√3
=300π3−50π3+25√3
=250π3+25√3cm2
Summary of Results
- Area of Minor Segment: 50π3−25√3cm2
- Area of Major Segment: 250π3+25√3cm2
The area of the sector formed by the angle at the center can be calculated using the formula:
Area of Sector=θ360∘×πr2
where θ is the angle in degrees and r is the radius of the circle.
=16×π×100
=100π6cm2
=50π3cm2
Next, we need to find the area of triangle OPQ, where O is the center of the circle. The formula for the area of a triangle when two sides and the included angle are known is:
Area of Triangle=12×a×b×sin(C)
where a and b are the lengths of the sides and C is the included angle.
=12×100×√32
=25√3cm2
The area of the minor segment can be calculated by subtracting the area of the triangle from the area of the sector:
Area of Minor Segment=Area of Sector−Area of Triangle
=50π3−25√3cm2
The area of the major segment can be found by subtracting the area of the minor segment from the total area of the circle:
Area of Circle=πr2=π(10)2=100πcm2
Area of Major Segment=Area of Circle−Area of Minor Segment
=100π−(50π3−25√3)
=100π−50π3+25√3
=300π3−50π3+25√3
=250π3+25√3cm2
- Area of Minor Segment: 50π3−25√3cm2
- Area of Major Segment: 250π3+25√3cm2
Topper's Solved these Questions
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Very Short Answer Question
12 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Revision Exercise Short Answer Question
12 Videos
- AREA RELATED TO CIRCLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA RELATED TO CIRCLESEXERCISE - Exercise 12 A
25 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
Similar Questions
A chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the minor and major segments. [Take π=314 and √3=1.732]
View SolutionA chord AB of a circle of radius 15 cm makes an angle of 60o at the centre of the circle. Find the area of the major and minor segment. (Take π=3.14, √3=1.73)
View Solution
Knowledge Check
A chord of a circle of radius 28 cm makes an angle of 90∘ at the centre. Find the area of the major segment.
A1456 cm2B1848 cm2C392 cm2D2240 cm2
A chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segment. (Use π=3.14)
View SolutionA chord of a circle of radius 30 cm makes an angle of 60∘ at the centre of the circle. Find the areas of the major segment. [Take π=3.14 and √3=1.732]
View SolutionA chord AB of a circle of radius 10cm makes a right angle at the centre of the circle. Find the area of the major and minor segments (Take π=3.14).
View SolutionA chord AB of a circle, of radius 14 cm makes an angle of 60∘ at the centre of the circle. Find the area of the minor segment of the circle.
View SolutionA chord PQ of a circle with radius 15 cm subtends an angle of 60∘ with the centre of the circle. Find the area of the minor as well as the major segment. (π=3.14,√3=1.73)
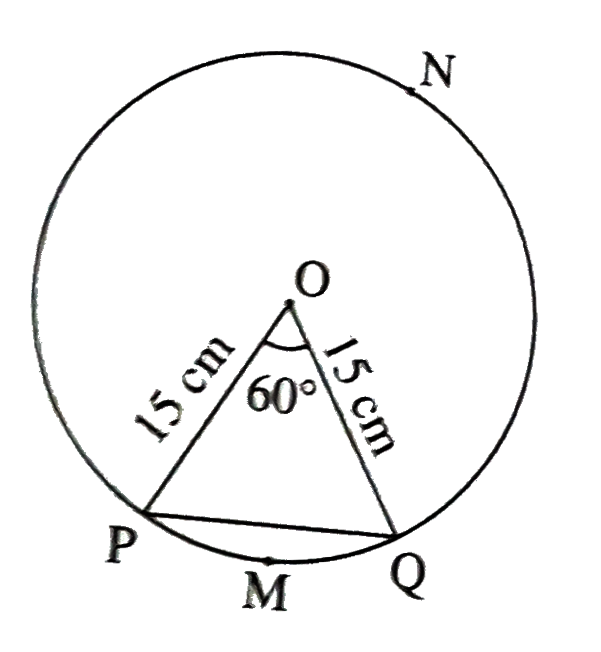
View SolutionA chord PQ of a circle4 with radius 15 cm subtends an angle of 60∘ with the centre of the circle.
Find the area of the inor as well as the major segement. (π=3.14,√3=1.73)
Given: r=15cm, θ=60∘
To find A(minor segment)
A(major segment)
View SolutionA chord of a circle of radius 6 cm subtends an angle of 60∘ at the centre of the circle. The area of the minor segment is (useπ=3.14)
View Solution
