Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
Video Solution
Text Solution
Let q0 be the initial charge on a capcitor, Let the charged capacitor be connected to an inductor of inductance L as you have studied in Section 7.8, this LC cirucit will sustain an oscillation with frequency.
ω(1=2πv=1√LC))
At an instant t. charge q on the capacitor and the current t are given by:
q(l)=q0cosωt
t(l)=−q0ωsinωt
Energy stored in the capacitor at time t is
UE=12CV2=12q2C=q202Ccos2(ωt)
Energy stored in the inductor at time t is
UM=12Lt2
=12Lq20ω2sin2(ωt)
=q202Csin2(ωt)(∵ω=1/√LC)
Sum of energies
UE+UM=q202C(cos2ωt+sin2ωt)
=q202C
This sum is constant in time as q0. and C , both are time-independent. Note that it is equal to the initial energy of the capacitor . why it is so? Think!
|
Topper's Solved these Questions
Similar Questions
Show that n the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionShow that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View Solution
Knowledge Check
In the circuit shown, the energy stored in 1μF capacitor is
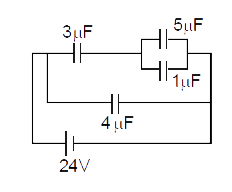 A40μJB64μJC32μJDnone of these
A40μJB64μJC32μJDnone of theseIn the circuit shown, the energy stored in 1μF capacitor is
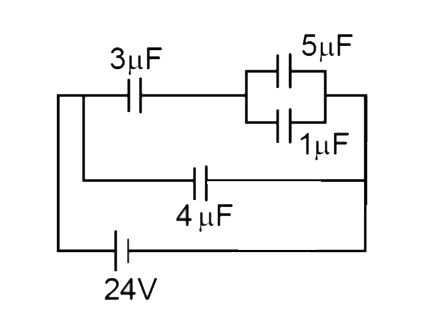 A40μJB64μJC32μJDnone
A40μJB64μJC32μJDnoneThe oscillation in LC, circuit is produced due to
Atransfer of energy between L and CBtransfer of resistance between L and CCtransfer of energy between diode and transistorDtransfer of energy between resistance and C
Choke coil | Oscillation in LC Circuit
View SolutionFind total energy stored in capacitors given in the circuit
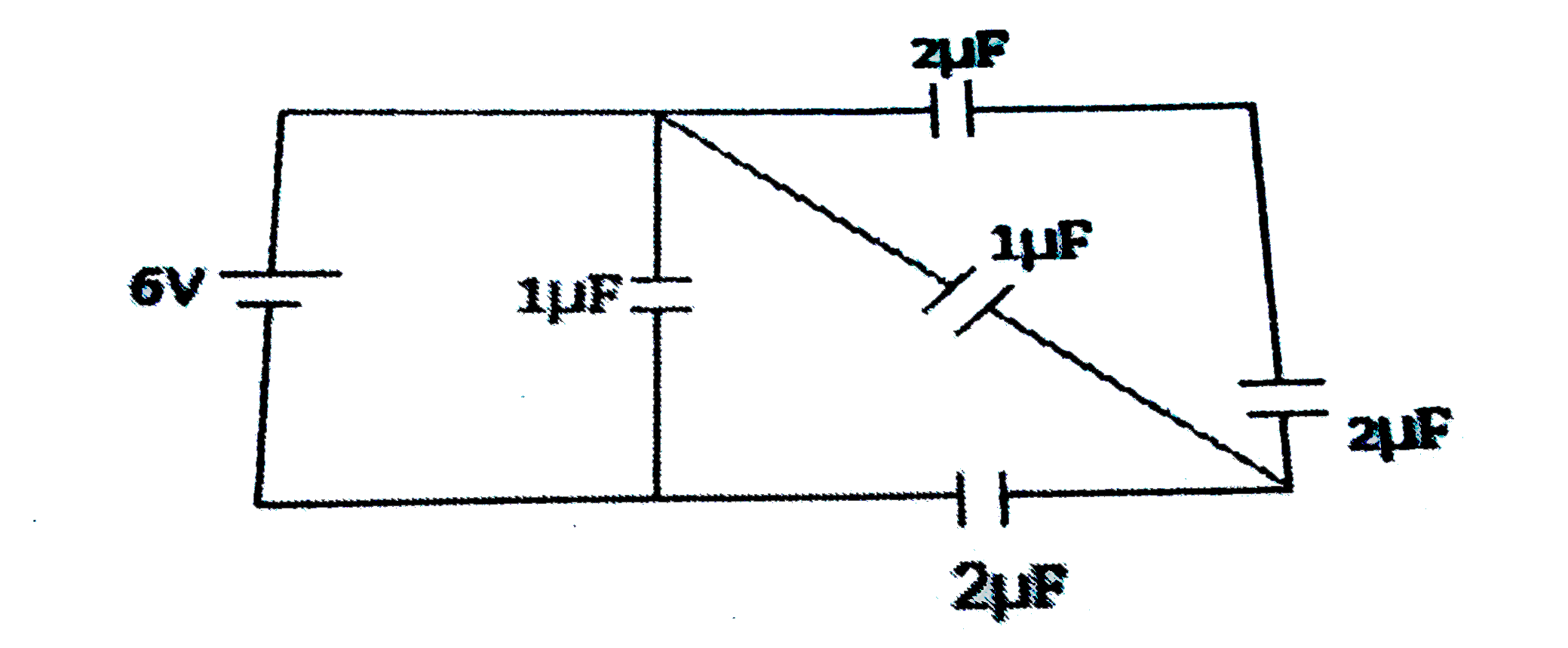
View SolutionFind total energy stored in capacitors given in the circuit.
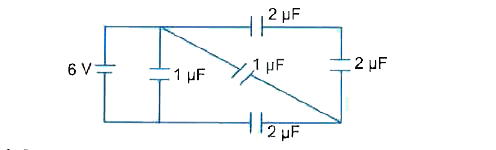
View SolutionWhat is the energy stored in a pure LC circuit ?
View SolutionIn a series circuit C=2μF,L=1mH and R=10Ω, when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
View Solution
