Show that n the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
To show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time, we can follow these steps:
Step 1: Define the energies stored in the capacitor and inductor
The energy stored in the capacitor EC is given by the formula:
EC=q22C
where q is the charge on the capacitor and C is the capacitance.
The energy stored in the inductor EL is given by:
EL=12LI2
where I is the current through the inductor and L is the inductance.
Step 2: Write the total energy
The total energy E in the LC circuit is the sum of the energies stored in the capacitor and inductor:
E=EC+EL=q22C+12LI2
Step 3: Express charge q and current I in terms of time
In an LC circuit undergoing free oscillations, the charge q on the capacitor varies with time as:
q(t)=q0sin(ωt)
where q0 is the maximum charge and ω is the angular frequency.
The current I can be expressed as the rate of change of charge:
I=dqdt=ddt(q0sin(ωt))=q0ωcos(ωt)
Step 4: Substitute q and I into the total energy equation
Substituting q(t) and I(t) into the total energy equation:
E=(q0sin(ωt))22C+12L(q0ωcos(ωt))2
Step 5: Simplify the energy equation
Expanding the terms:
E=q20sin2(ωt)2C+12Lq20ω2cos2(ωt)
Step 6: Use the relationship between ω, L, and C
We know that:
ω2=1LC
Substituting this into the energy equation:
E=q20sin2(ωt)2C+12Lq20(1LC)cos2(ωt)
This simplifies to:
E=q20sin2(ωt)2C+q20cos2(ωt)2C
Step 7: Factor out the common term
Factoring out q202C:
E=q202C(sin2(ωt)+cos2(ωt))
Step 8: Apply the Pythagorean identity
Using the identity sin2(θ)+cos2(θ)=1:
E=q202C⋅1=q202C
Conclusion
The total energy E is constant over time, showing that the sum of energies stored in the capacitor and inductor remains constant in free oscillations of an LC circuit.
The energy stored in the capacitor EC is given by the formula:
EC=q22C
where q is the charge on the capacitor and C is the capacitance.
EL=12LI2
where I is the current through the inductor and L is the inductance.
The total energy E in the LC circuit is the sum of the energies stored in the capacitor and inductor:
E=EC+EL=q22C+12LI2
In an LC circuit undergoing free oscillations, the charge q on the capacitor varies with time as:
q(t)=q0sin(ωt)
where q0 is the maximum charge and ω is the angular frequency.
I=dqdt=ddt(q0sin(ωt))=q0ωcos(ωt)
Substituting q(t) and I(t) into the total energy equation:
E=(q0sin(ωt))22C+12L(q0ωcos(ωt))2
Expanding the terms:
E=q20sin2(ωt)2C+12Lq20ω2cos2(ωt)
We know that:
ω2=1LC
Substituting this into the energy equation:
E=q20sin2(ωt)2C+12Lq20(1LC)cos2(ωt)
This simplifies to:
E=q20sin2(ωt)2C+q20cos2(ωt)2C
Factoring out q202C:
E=q202C(sin2(ωt)+cos2(ωt))
Using the identity sin2(θ)+cos2(θ)=1:
E=q202C⋅1=q202C
The total energy E is constant over time, showing that the sum of energies stored in the capacitor and inductor remains constant in free oscillations of an LC circuit.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Solved Examples (b)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Short Answer Qusetions
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:II Focus multiple choice question
Explore 5 Videos
Similar Questions
Knowledge Check
In the circuit shown, the energy stored in 1μF capacitor is
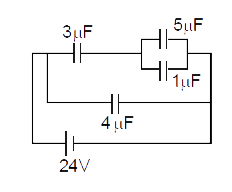 A40μJB64μJC32μJDnone of these
A40μJB64μJC32μJDnone of theseIn the circuit shown, the energy stored in 1μF capacitor is
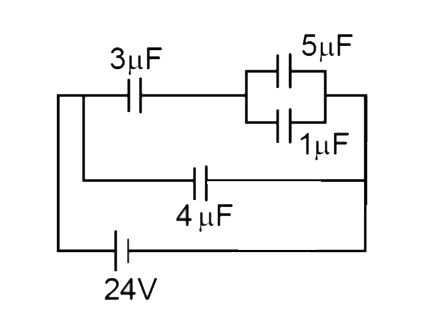 A40μJB64μJC32μJDnone
A40μJB64μJC32μJDnoneThe oscillation in LC, circuit is produced due to
Atransfer of energy between L and CBtransfer of resistance between L and CCtransfer of energy between diode and transistorDtransfer of energy between resistance and C
Find total energy stored in capacitors given in the circuit
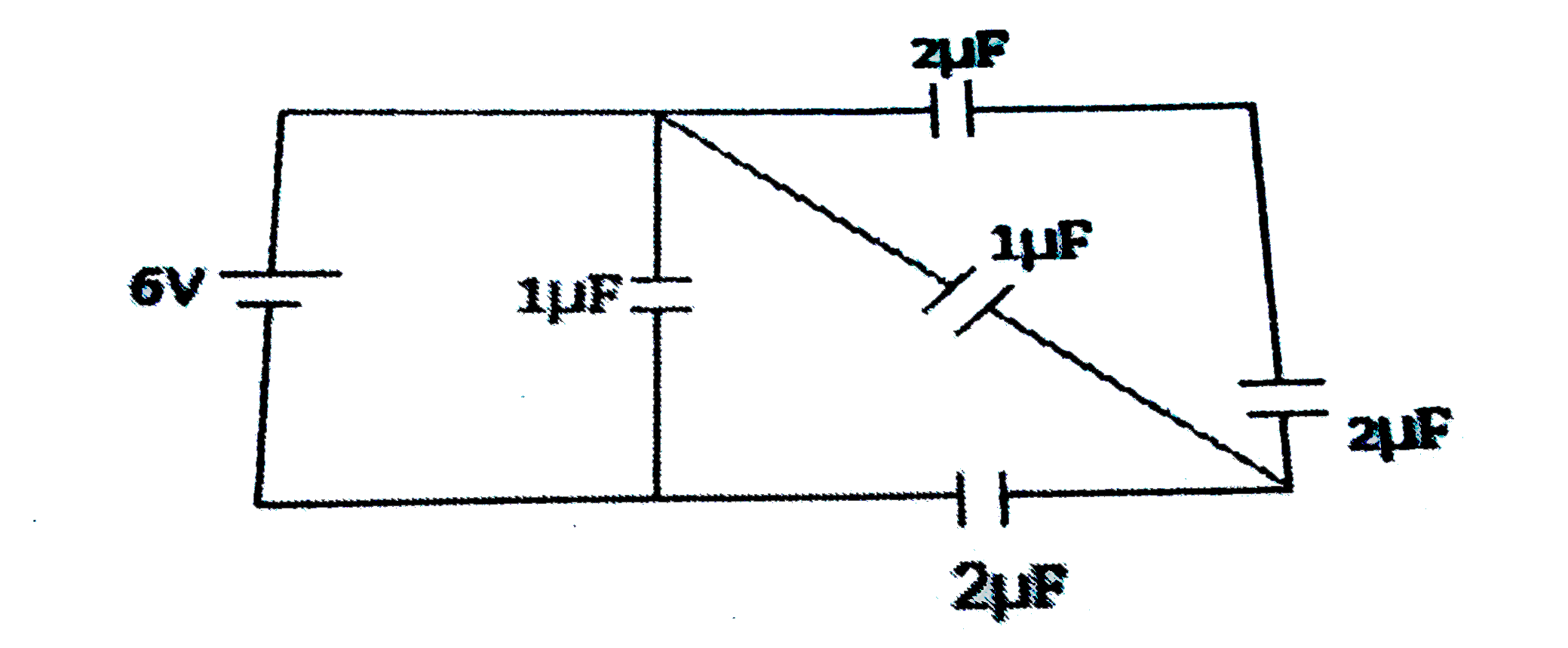
View SolutionFind total energy stored in capacitors given in the circuit.
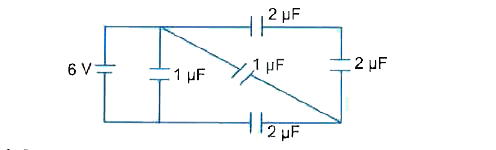
View SolutionWhat is the energy stored in a pure LC circuit ?
View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionIn a series circuit C=2μF,L=1mH and R=10Ω, when the current in the circuit is maximum, at that time the ratio of the energies stored in the capacitor and the inductor will be
View Solution

